模型同構是一個數學術語。
基本介紹
- 中文名:模型同構
- 外文名:isomorphism of models
- 所屬學科: 數學
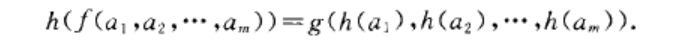
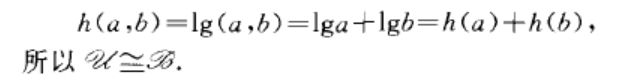

模型同構是一個數學術語。
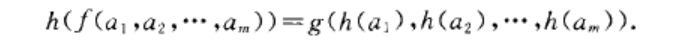
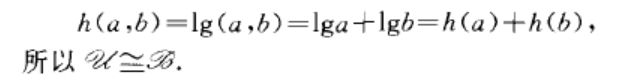
模型同構是一個數學術語。描述模型同構(isomorphism of models)模型論術語.指兩模型間的一種等價關係.語言丫中的模型}l=CA,{r},}f},{:})和.}= CB,{、},fig},{d})同構(記...
模同構是一種特殊的模同態,假設f是模M到模N的同態,若f時一一的並且是映上的,則f為模M到模N的同構。兩個同構的模,從模的結構來看,它們沒有什麼區別。模同構具有一個性質,即若f為模M到模N的同態,則f的逆映射f^(-1)也是同構。廣義模同構是一種廣義模同態。預備知識 模的同態映射 設M 和M' 均...
模型同構嵌入(isomorphic embedding of mo -dell)一種特殊的子模型關係.設ail , .是丫的兩個模型,如果存在一個從o到居的一個子模型y'的同構映射h,即h : u-,且省里留,則稱模型召了可以同構嵌人留中,此時也稱男是那的一個同構擴張.例如,令oil=(N,十,0),= (N, " ,1),其中N為自然數集....
(1)LDBMS(Local DBMS),局部站點上的資料庫管理系統,其功能是建立和管理局部資料庫,提供站點自治能力,執行局部套用及全局查詢的子查詢。在同構並同質時,模式和操作都不需要轉換,可直接執行操作,所以其功能被弱化。(2)GDBMS(Global DBMS),全局資料庫管理系統,主要功能是提供分布透明性,協調全局事務的執行,...
同構思想(idea of isomorphism)是數學的基本思想之一。當著兩個集合在某種意義下同構,則可以把對某個集合的研究,完全地轉化為對另一集合的研究.例如對實數序偶的加法和平面向量的加法而言,序偶集合和向量集合是同構的.因而就加法來說,完全可以把對平面向量的研究轉化為對實數序偶的研究.在數學中最簡單而常用的...
標準模型(standard model)是指滿足一定條件的模型,在以自然數、有理數、實數、複數等標準的數學結構的研究中,當我們試圖通過公理化,把它們置入一階謂詞演算中以構成一階系統時,就能發現該系統的模型之間結構可以相同也可以不相同。通常把與原來的結構同構的模型稱為標準模型,反之稱為非標準模型。其定義為:令S為...
同構模型 同構模型(isomorphic model)是1990年公布的自動化科學技術名詞。公布時間 1990年經全國科學技術名詞審定委員會審定發布。出處 《自動化名詞》第一版。
用模型論方法的證明,一般是基於如下事實:若理論T有一個遞歸可枚舉的公理集,並且T是完備的,則理論T是可判定的.而理論T的完備性,很多是通過模型論方法證明的.例如,許多證明都用到了以下定理:若理論T沒有有窮模型,並且存在某個無窮基數a,使T為a範疇的(即T的任何兩個基數為a的模型是同構的),則T為完備...
Keisler-Shelah iso-morphism theorem)初等等價模型的代數判定定理.設ou},c}是語言獷的模型。則au三劣的充分必要條件是:存在一非空足碼集1及1上的超濾子D,使TTD0?}l- TTD.}.該定理把兩個模型的“初等等價”的模型論概念轉化為其超冪的同構的代數概念,因而有助於模型論問題與代數問題的溝通.
第三章 模型論的形式語言 3.1 形式邏輯中的命題演算 3.2 一階邏輯簡介 3.3 命題演算的模型論的補充性質 3.4 模型論的形式語言 3.5 模型論的式子和它們的構成 3.6 模型論的式子推演 練習題 第四章 模型的基本性質 4.1 形式語言的解釋與模型 4.2 模型的同構,同態,子模型,擴張,膨脹,歸約...
二、氣的科學模型與現代科學本質 三、現代的場 四、氣與場同型 五、陰陽五行模型與量子場論模型同構 第四章 氣化的磁共振模型 第一節 古代中國的太極模型 第二節 氣化的太極模型與量子場模型同構 一、模擬氣化的太極模型 二、電子、量子運動模型與太極模型同構 三、物質的磁性、極性與太極模型同構 四、外加...
可傳模型(transitive model)是一類標準模型。定義 若M為集合論語言的一個標準模型且M可傳,則稱M為一個可傳模型.可傳模型是集合論相容性與獨立性證明中最常採用的一類模型.模型的可傳性可保證模型滿足外延公理,也可保證許多集合論概念絕對.由崩塌數學辭海第4卷定理,任意良基模型均同構於一個可傳模型.可數的可...
亨森引理(Henson lemma)是關於模型同構的一個引理,其可判定初等價結構是否同構。簡介 亨森引理是關於模型同構的一個引理。該引理斷言:對於每個其常量及關係個數少於card⁺(X)(card⁺(X)是card(X)的後繼基數)的一階語言L,若A與B是L的初等價結構,它的定義域與關係是多擴大*X的內實體,並且card(A)=...
範疇的是模型論的基本概念之一。指理論J的任意兩個模型都是同構的。兩個模型同構,實質上可以看作一個模型。因此,從結構的觀點看,一個理論是範疇的,指的是該理論在同構的意義下,實質上只有一個模型。範疇性通過對形式理論的模型性質的某種規定來刻畫形式理論本身的性質。然而,只要J具有至少一個無限模型,它便...
範疇性(categoricity)是理論的某個基數的模型都同構的一種特性。設L為一可數語言,T是L中的完全理論。如果T恰有一個可數模型(在同構意義下),則稱T為ω範疇的。概念 範疇性(categoricity)是理論的某個基數的模型都同構的一種特性。設L為一可數語言,T是L中的完全理論。如果T恰有一個可數模型(在同構意義下),...
如歐幾里得幾何公理體系完備性的證明,即由該體系的每一模型都與實數模型同構而得到它的所有模型同構。對任何一個公理體系要求它必須是相容的,最好是獨立的,至於完備性則可根據需要而定。例如,歐幾里得幾何體系是相容的、獨立的並且是完備的,所以歐幾里得幾何有豐富的內容,它刻畫了歐幾里得空間,而絕對幾何體系是不...
完備的公理系統要求它的所有不同模型都是互相同構的.可以嚴格證明,歐幾里得幾何公理系統和羅巴切夫斯基幾何公理系統都是完備的公理系統。幾何公理系統模型的同構 幾何公理系統模型的同構(isomorphism of geometric axiom system model)指對同一幾何系統不同模型之間的某種關係的描述,設AX表示由若干個公理所組成的一個公理...
模型也可以用來顯示一個公理在系統中的獨立性。通過構造除去一個特定公理的子系統的正確模型,我們表明該省去的公理是獨立的,若它的正確性不可以從子系統得出。兩個模型被稱為同構,如果它們的元素可以建立一一對應,並且以一種保持它們之間的關係的方式。一個其每個模型都同構於另一個的公理系統稱為範疇式的,而...
有可能相對化這個完整構造於ZF(或者有時它的片段)的某個傳遞模型M。在這種情況下我們通過套用上述構造於M內部而構造布爾值模型M。對傳遞模型的限制是不嚴重的,因為Mostowski塌陷引理蘊涵了所有合理的(良基的外延)模型同構於傳遞模型。(如果模型M不是傳遞事物而使其變得更加雜亂,因為M對什麼意味著是“函式”或“集合...
初等類 初等類(elementary class)一個理論的模型組成的模型類.初等類一個理論的模型組成的模型類.設K是語言牙的一族模型(同構的模型只算作一個),如果存在牙中的一個理論T,使K恰由T的一切模型組成,則稱K為一個初等類.如果存在牙中的一個語句a,使K恰由a的一切模型組成,則稱K為一個基本初等類 ...
早期建立的細觀尺度偶應力板理論多限於各向同性C0偶應力模型(含兩類位移和至少含兩個材料細觀參數),與經典梁、板模型差異很大。近期推出的各向同性梁、板的C1對稱修正偶應力模型含一類位移和一個材料細觀參數,建立的模型與經典梁、板模型同構,尺度效應直觀,但是,修正偶應力理論只能用於各向同性材料。本項目將...
時空型也名空間型,指空間的兩個結構體之間的同構關係。 時空型決策所指的空間是三度空間,除了肉眼空間,還包括更大的巨觀空間和更小的微觀空間。這樣的三度空間,還在時間線上不斷變換著運動的角度,構成複雜多變的時空模型。根據複雜多變的時空模型進行的決策,是時空型決策。空間型決策 肉眼可見的空間最容易被...
設秘,歷是語言丫的模型,如果存在一個映射h:A->B,對驢的任意公式抓xl,xz, "..x‑和對任意的n元組a,a2,二,a‑ E A有au 甲壓,az, w,a,,若且唯若. pha, , hat, ,hand,則稱映射h是從ou到驪的初等嵌人.並稱ou能初等嵌人男中.這也就是說,ou與W的一個初等子模型同構,即a三h...
例如,有限幾何某些模型的自同構群在一般意思下不是「對稱群」,儘管其亦會保留對稱性。其保留著點集族,而非點集(或「物件」)本身。見pattern groups。如上面所述,空間自同構的群會形成一於其內物件之群作用。對於一給定之幾何空間內的一給定之幾何形狀,考慮如下之等價關係:兩個空間自同構為等價的若且唯若兩...
原有的複雜系統和我們給出的簡化系統彼此的關係是原型與模型的同構關係:兩者具有同樣的輸入與輸出的關係,表明兩者在某種功能方面是相同的,但這不等於說兩者完全相同。黑箱方法儘管有這種局限性,但依然得到廣泛的套用,現已發展成為控制理論的一個重要方法──系統辨識。套用這種方法,可以通過外部觀測所獲得的數據,...
.證明每個這樣的系統所相應的模型都是同構的..尋找這樣一種方法,藉助於它,可在有限步驟內判定任一命題的可證明性. 希爾伯特為具體實施其規劃而創立證明論,即元數學理論.它著眼於整個形式系統,並以“證明”本身作為研究對象.希爾伯特主義派有三種數學系統:.非形式化的數學系統G:即普通的數學系統,在其中允許使用...
而常用的一個這樣的概念是同構,然而同構的概念又太強,因為同構的結構本質上和形式上都是相同的。於是,人們希望有一個介於同態和同構之間的概念,在這一探索過程中,互模擬等價被引入。定義 模態邏輯中常常把互模擬定義在克里普克模型上。定義 令 M = (W , R, V ) 和 M ′= (W ′, R′,V′)是兩個...
強調收發訊息的對象的結構組織,順序圖和協作圖是同構的,這意味著它們可以互相轉換。活動圖(activity diagram)描述系統元素的活動,是一種特殊的狀態圖,它展現了在系統內從一個活動到另一個活動的流程。活動圖專注於系統的動態視圖,它強調對象間的控制流程,對於系統的功能建模特別重要。用例視圖(use case view)...
1、空間的有理上同調即是其蘇利文極小模型的上同調;2、 的不可分元素的空間即是 的有理同倫群的對偶;3、有理同調的懷特海德積即是導子d 的“二次部分”的對偶;4、兩空間的有理同倫型相同若且唯若其蘇利文極小模型同構;5、對任意 且所有 維數有限的蘇利文代數都存在一個單連通的拓撲空間 與之對應...
