概自守函式(almost-automorphic function)是較概周期函式更弱的一類函式。
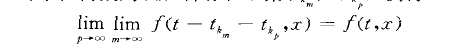

概自守函式(almost-automorphic function)是較概周期函式更弱的一類函式。
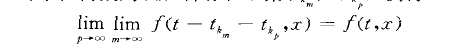

概自守函式(almost-automorphic function)是較概周期函式更弱的一類函式。概自守函式(almost-automorphic function)較概周期函式更弱的一類函式.如果對於R”的任,緊子集D...
自守函式(automorphic function)是圓函式、雙曲函式、橢圓函式等概念的推廣.設X是Cⁿ中有界連通開集,G是X賦以緊開拓撲後的自同構(即雙全純雙射)群,Γ是G的離散子群,若一個亞純函式f在Γ作用下不變,則稱為(關於Γ的)自守函式....
1961年博赫納又引人了比玻爾函式更一般的概自守函式。博赫納在1932 年給出了博赫納正定函式定理,即連續復值函式 能表示成傅立葉-斯蒂爾傑斯積分 ,其中 ,若且唯若對任意有限點,,和復常數 時才成立。這一判別準則在機率論中有不...
研究了S^p加權偽概自守函式、μ-加權偽概自守(周期)函式和μ-S^p加權偽概自守函式的基本性質,並套用於半線性微分方程的研究。研究了時標系統的回覆性問題,給出偽概周期函式在時標系統上和實數系統上的關係,建立了時標上的...
建立了新型的概自守函式的複合定理以及非自治抽象發展方程偽概自守解的存在唯一性定理,解答了概周期與概自守理論中的一些基本問題;在無窮維空間構架下,解答了一個強連續運算元半群的範數函式的反問題;等。
證明了線上性系統近似可控的情況下,Hilbert空間中一非線性混合分數階鬆弛方程在這一控制函式作用下也是近似可控的。利用測度理論,我們給出了偽概自守函式的複合定理,並由此給出了由預解運算元控制的半線性微分方程解的偽概自守性質。
Banach空間中多元非線性擾動下的奇異非線性脈衝微分方程的邊值問題,方程的f漸近性及相關的f發散性和Bregman發散性的特徵和相互關係,Banach空間中非局部非線性分數階微分方程mild解的存在性及正則化條件,加權Stepanov類偽概自守函式的複合...
利用測度理論,證明了偽概自守函式的複合定理,由此給出了一類半線性分數階微分方程的偽概周期解和偽概自守解存在唯一的條件。利用逐步構造近似解的方法,證明了當相關半群為緊半群,擾動函式為Caratheodory型時,不變流存在的充要條件是...
Chapter 2 is preliminaries, mainly including some definitions and basic properties on strongly continuous semigroups, integrated semigroups and pseudo al-most automorphic functions.主要包括強連續半群、積分半群與擬概自守函式的...
