概周期向量函式(almost periodic vector func-dons)是一類特殊的向量函式。
基本介紹
- 中文名:概周期向量函式
- 外文名:almost periodic vector func-dons
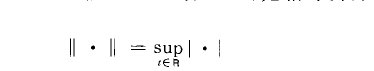

概周期向量函式(almost periodic vector func-dons)是一類特殊的向量函式。
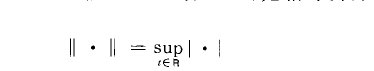
概周期向量函式(almost periodic vector func-dons)是一類特殊的向量函式。如果向量值函式f(t>fi (t) ),.fz (t) , ... ,.fn (t) T的每一元素.f=(t>(2=...
在高維歐幾里得空間中,也可以定義類似的概周期向量函式。按照定義,所有周期函式都是概周期函式。值域在複平面上的概周期函式與三角多項式函式有密切關係。哈那德·玻爾首先注意到這類型的函式是在研究有限項狄利克雷級數的時候。當把黎曼ζ函式:ζ(s) 截出有限項後,得到的是一些形如 的項。其中的 。如果只考...
(x,t)是t的概周期函式。這裡x是n維向量,?(x,t)是n維向量函式。概周期微分方程的發展歷史不長,但由於它具有實際背景(如天體力學和非線性振動的問題)而顯示出生命力。特別是,1945年,A.H.柯爾莫哥洛夫利用無理性條件,指出哈密頓系統具有擬周期解。1963年,Β.И.阿諾爾德又給出嚴格證明,由此證明了太陽系不...
概周期函式的理論首先是由丹麥數學家玻爾(Bohr,H.)在1924-1926年建立起來的.在20世紀20-30年代經一批數學家的努力,玻爾的理論有了進一步的發展,包括在群上的調和分析理論以及由博赫納(Bochner,S.)於1933年所建立的巴拿赫空間的向量值概周期函式的理論.往後的發展更密切地聯繫著常微分方程、穩定性理論以及動力系統...
《幾類新的函式空間及其在反問題和控制論中的套用》是依託哈爾濱工業大學,由張傳義擔任項目負責人的面上項目。項目摘要 本項目要建立和完善幾個具體的函式空間理論,其中包括偽概周期函式空間,由極限功率函式和緩慢振盪函式所生成的代數,它們的Gelfand空間的結構.在很一般意義下, 這些函式的Bochner-Fejer表示,Fourier...
玻爾一諾伊格鮑爾理論(theory of Bohr-Neuge-bauer)闡明常係數線性微分方程有界解為概周期解的重要理論。玻爾一諾伊格鮑爾理論,闡明常係數線性微分方程有界解為概周期解的重要理論.玻爾(Bohr , H.)最早指出:概周期函式f'(t)的積分 是概周期函式的充分必要條件是,F (t)對一切tER為有界.這就解決了最簡單的一階...
最小範數解(minimum norm)是概周期解存在性的一個重要概念。線性微分方程論對常係數非齊次。不難看出,如果n維連續向量f}(t>葬n,則方程的有界解的集合在、維空間是一個不含坐標原點的凸集,這個凸集中必有元素具有最小範數.該元素所對應的微分方程的解稱為具有最小範數解.這個事實對一般非線性微分方程dx/dt...
博赫納積分(Bochner integral)是按勒貝格積分方式定義的一種常用的向量值函式的積分。博赫納積分是勒貝格積分在向量值函式情形的直接推廣,是由博赫納(S.Bochner)在1932年建立的,這種積分在向量值測度理論、運算元理論、機率論、隨機過程以及巴拿赫空間幾何理論等許多數學分支中有廣泛的套用。基本介紹 設 是完備的σ有限...
是概周期方陣, 是概周期向量,且(1)具有指數型二分性,那么,非齊次線性概周期方程系 存在惟一概周期解,它可表達為 且 ,同時 時標動力學方程的指數型二分性 定義 考慮線性非自治時標動力學方程 其中, 。現在給出線性非自治時標動力學方程上指數型二分性的概念。定義1 若存在投影 和正常數 使得...
富里埃變換將函式的時域(紅色)與頻域(藍色)相關聯。頻譜中的不同成分頻率在頻域中以峰值形式表示。傅立葉變換源自對富里埃級數的研究。在對富里埃級數的研究中,複雜的周期函式可以用一系列簡單的正弦、餘弦波之和表示。富里埃變換是對富里埃級數的擴展,由它表示的函式的周期趨近於無窮。富里埃變換在數據科學、...
從數學的角度出發,以非線性分析為工具,探討了集值函式的若干性質,如重新定義了可微性,創新性的探討了概周期性概念及性質等,特別,將問題建立在時間標架上,從方法上統一了離散統與連續統的相關問題的研究,同時探討了相應的模糊函式問題。獲得了不連續集值運算元的不動點、最佳逼近點以及模糊不動點的存在性的新...
