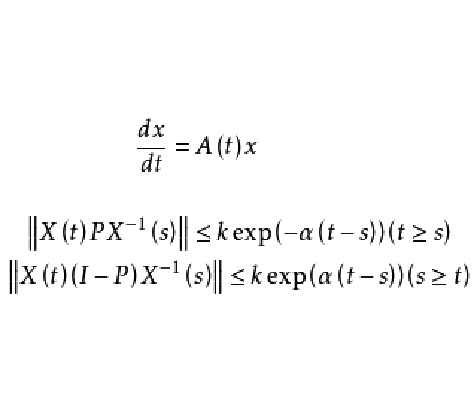指數型二分性

指數型二分性(exponential dichotomy and spectrum)是關於線性微分方程的一種重要性質。指數型二分性理論是線性自治方程的雙曲率概念線上性非自治方程中的推廣，並且在非自治方程分析中占有重要的地位。線性微分方程的指數型二分性理論最早可以追溯至Perron利用指數型二分性研究了線性微分方程的穩定性和非線性微分方程有界解的存在性。1934年，Li建立了線性差分方程上指數型二分性理論。指數型二分性理論已經在微分方程和差分方程定性與穩定性研究中發揮著重要的作用，並以其豐富的理論思想和複雜的數學技巧套用到數學的各個研究領域之中。

基本介紹

• 中文名：指數型二分性
• 外文名：exponential dichotomy and spectrum
• 所屬學科：數學
• 屬性：關於線性微分方程的一種重要性質
• 所屬問題：概周期常微分方程

基本介紹

指數型二分性是關於線性微分方程的一種重要性質。設齊次線性微分方程系

在 上連續，其中 是 階方陣，如果存在投影 及正的常數 使

其中 是(1)的基本解方陣，則稱(1)在R上具有指數型二分性。全軸上線性系統的指數型二分性在穩定性理論中是一種有力的工具，在概周期微分方程系的研究中也是非常有用的工具，如果 是概周期方陣， 是概周期向量，且(1)具有指數型二分性，那么，非齊次線性概周期方程系

存在惟一概周期解，它可表達為

且 ，同時

時標動力學方程的指數型二分性

定義

考慮線性非自治時標動力學方程

其中， 。

現在給出線性非自治時標動力學方程上指數型二分性的概念。

定義1 若存在投影 和正常數 使得對於(2)的基解矩陣 滿足

則稱(2)在 上具有指數型二分性，如果(2)中 ，則稱(2)在 上具有通常二分性。

註記1 若令 ，定義1與經典的線性微分方程上指數型二分性概念相一致，若令 ，則能夠轉化為線性差分方程上指數型二分性，即

註記2 若選擇一個恰當的基解矩陣，則投影 和 能夠分別寫成下面的形式

這裡， 是一個 階單位矩陣， 是一個 階單位矩陣。實際上，一定存在一個非奇異的矩陣T使得 ，那么(3)變為下面的形式

設 ，顯然有 也是一個基解矩陣。

註記3 若 ，則對於任意的 且 ， 是一個嚴格增函式且 ，而 是一個嚴格的減函式且 。因而對於 ，有

指數型二分性的基本性質

下面主要介紹線性非自治時標動力學方程上指數型二分性的一‘些基本性質。

指數型二分性存在的充要條件

定理1線性非自治時標方程(2)具有指數型二分性的充要條件是 是一致有界的且存在正常數 使得對於任意 ，有

定理2 假設下面的條件成立：

(i) 存在正常數 使得對於任意 有

(ii) (2)是有界增長的，即存在正常數 使得

則(2)在 上具有指數型二分性。

引理1 若(2)在 上具有指數型二分性，其中 ，則(2)在 上具有指數型二分性且具有相同的投影P和指數估計 。

定理3 假設 是有界的，(2)在 上滿足指數型二分性的充要條件是存在正常數 使得(2)的任意一個解對於 滿足