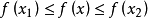基本介紹
- 中文名:極值定律
- 外文名:crest theorem
- 套用:微積分
內容,證明,有界性定理的證明,極值定理的證明,
內容
在數學分析中,極值定理說明如果實函式f(x)在閉區間[a,b]上是連續函式,
有界閉區域上的二元連續函式也有類似於一元函式的最值定理。
同理,根據有界性定理,可得在閉區間[a,b]內的連續函式f在該區間上有界,即存在實數m和M,使得:m≤f(x)≤M。
證明
證明極值定理的基本步驟為:
1.證明有界性定理。
2.尋找一個序列,它的像收斂於f(x)的最小上界。
3.證明存在一個子序列,它收斂於定義域內的一個點。
4.用連續性來證明子序列的像收斂於最小上界。
5.同理證明最大下界。
有界性定理的證明
假設函式f(x)在區間[a,b]內沒有上界,則根據實數的阿基米德原理,對於每一個自然數n,都存在[a,b]內的一個xn,使得f(xn) > n。這便定義了一個序列{xn}。由於[a,b]是有界的,根據波爾查諾-魏爾施特拉斯定理,可推出存在{xn}的一個收斂的子序列{Xnk}。把它的極限記為X;由於[a,b]是閉區間,它一定含有X;因為f(x)在X處連續,我們知道{f(Xnk)}收斂於實數f(X)。但對於所有的k,都有f(Xnk) > nk ≥ k,這意味著{f(Xnk)}發散於無窮大和X收斂相矛盾。因此,f在[a,b]內有上界。
極值定理的證明
我們現在證明函式f(x)在區間[a,b]內有最大值。根據有界性定理,f(x)有上界,因此,根據實數的戴德金完備性,f的最小上界M存在。我們需要尋找[a,b]內的一個d,使得M = f(d)。設n為一個自然數。由於M是最小上界,M – 1/n就不是f(x)的最小上界。因此,存在[a,b]內的dn,使得M – 1/n < f(dn)。這便定義了一個序列{dn}。由於M是f的一個上界,我們便有M – 1/n < f(dn) ≤ M,對於所有的n。因此,序列{f(dn)}收斂於M。
根據波爾查諾-魏爾施特拉斯定理,可知存在一個子序列{Dnk},它收斂於某個d,且由於[a,b]是閉區間,d位於[a,b]內。因為f在d處連續,所以序列{f(Dnk)}收斂於f(d)。但{f(Dnk)}是{f(dn)}的一個子序列,收斂於M,因此M = f(d)。所以,f在d處取得最小上界M。