棋盤覆蓋問題，是一種編程問題。
如何套用分治法求解棋盤覆蓋問題呢？分治的技巧在於如何劃分棋盤，使劃分後的子棋盤的大小相同，並且每個子棋盤均包含一個特殊方格，從而將原問題分解為規模較小的棋盤覆蓋問題。k>0時，可將2^k×2^k的棋盤劃分為4個2^（k-1）×2^（k-1）的子棋盤，如圖4.11(a)所示。這樣劃分後，由於原棋盤只有一個特殊方格，所以，這4個子棋盤中只有一個子棋盤包含該特殊方格，其餘3個子棋盤中沒有特殊方格。為了將這3個沒有特殊方格的子棋盤轉化為特殊棋盤，以便採用遞歸方法求解，可以用一個L型骨牌覆蓋這3個較小棋盤的會合處，如圖4.11(b)所示，從而將原問題轉化為4個較小規模的棋盤覆蓋問題。遞歸地使用這種劃分策略，直至將棋盤分割為1×1的子棋盤。
基本介紹
- 中文名：棋盤覆蓋問題
- 棋盤：二維數組board[size][size]
- 處理方法：遞歸處理
- 範疇：編程
問題,想法,算法實現,算法分析,
問題
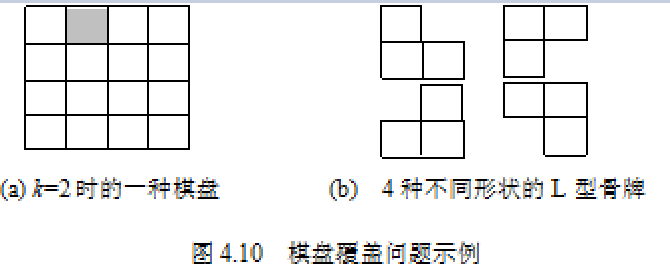
在一個2^k×2^k （k≥0）個方格組成的棋盤中，恰有一個方格與其他方格不同，稱該方格為特殊方格。顯然，特殊方格在棋盤中可能出現的位置有4^k種，因而有4^k種不同的棋盤，圖4.10(a)所示是k=2時16種棋盤中的一個。棋盤覆蓋問題（chess cover problem）要求用圖4.10(b)所示的4種不同形狀的L型骨牌覆蓋給定棋盤上除特殊方格以外的所有方格，且任何2個L型骨牌不得重疊覆蓋。
想法
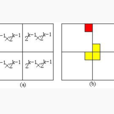
如何套用分治法求解棋盤覆蓋問題呢？分治的技巧在於如何劃分棋盤，使劃分後的子棋盤的大小相同，並且每個子棋盤均包含一個特殊方格，從而將原問題分解為規模較小的棋盤覆蓋問題。k>0時，可將2^k×2^k的棋盤劃分為4個2^（k-1）×2^（k-1）的子棋盤，如圖4.11(a)所示。這樣劃分後，由於原棋盤只有一個特殊方格，所以，這4個子棋盤中只有一個子棋盤包含該特殊方格，其餘3個子棋盤中沒有特殊方格。為了將這3個沒有特殊方格的子棋盤轉化為特殊棋盤，以便採用遞歸方法求解，可以用一個L型骨牌覆蓋這3個較小棋盤的會合處，如圖4.11(b)所示，從而將原問題轉化為4個較小規模的棋盤覆蓋問題。遞歸地使用這種劃分策略，直至將棋盤分割為1×1的子棋盤。
算法實現
下面討論棋盤覆蓋問題中數據結構的設計。
（1）棋盤：可以用一個二維數組board[size][size]表示一個棋盤，其中，size=2^k。為了在遞歸處理的過程中使用同一個棋盤，將數組board設為全局變數；
（2）子棋盤：整個棋盤用二維數組board[size][size]表示，其中的子棋盤由棋盤左上角的下標tr、tc和棋盤大小s表示；
（3）特殊方格：用board[dr][dc]表示特殊方格，dr和dc是該特殊方格在二維數組board中的下標;
（4） L型骨牌：一個2^k×2^k的棋盤中有一個特殊方格，所以，用到L型骨牌的個數為(4^k-1)/3，將所有L型骨牌從1開始連續編號，用一個全局變數t表示。
設全局變數t已初始化為0，分治法求解棋盤覆蓋問題的算法用C++語言描述如下：
void ChessBoard(int tr, int tc, int dr, int dc, int size)
{
int s, t1; //t1表示本次覆蓋所用L型骨牌的編號
if (size == 1) return; //棋盤只有一個方格且是特殊方格
t1 = ++t; // L型骨牌編號
s = size/2; // 劃分棋盤
if (dr < tr + s && dc < tc + s) //特殊方格在左上角子棋盤中
ChessBoard(tr, tc, dr, dc, s); //遞歸處理子棋盤
else{ //用 t1號L型骨牌覆蓋右下角，再遞歸處理子棋盤
board[tr + s - 1][tc + s - 1] = t1;
ChessBoard(tr, tc, tr+s-1, tc+s-1, s);
}
if (dr < tr + s && dc >= tc + s) //特殊方格在右上角子棋盤中
ChessBoard(tr, tc+s, dr, dc, s); //遞歸處理子棋盤
else { //用 t1號L型骨牌覆蓋左下角，再遞歸處理子棋盤
board[tr + s - 1][tc + s] = t1;
ChessBoard(tr, tc+s, tr+s-1, tc+s, s);
}
if (dr >= tr + s && dc < tc + s) //特殊方格在左下角子棋盤中
ChessBoard(tr+s, tc, dr, dc, s); //遞歸處理子棋盤
else { //用 t1號L型骨牌覆蓋右上角，再遞歸處理子棋盤
board[tr + s][tc + s - 1] = t1;
ChessBoard(tr+s, tc, tr+s, tc+s-1, s);
}
if (dr >= tr + s && dc >= tc + s) //特殊方格在右下角子棋盤中
ChessBoard(tr+s, tc+s, dr, dc, s); //遞歸處理子棋盤
else { //用 t1號L型骨牌覆蓋左上角，再遞歸處理子棋盤
board[tr + s][tc + s] = t1;
ChessBoard(tr+s, tc+s, tr+s, tc+s, s);
}
}
算法分析
設T(k)是算法ChessBoard覆蓋一個2^k×2^k棋盤所需時間，從算法的劃分
策略可知，T(k)滿足如下遞推式：
T(k) = 1 當k=0時
T(k) = 4T(k-1) 當k>0時
解此遞推式可得T(k)=O(4^k)。
