基本介紹
- 中文名:條件期望
- 外文名:Conditional expectation
- 別稱:條件數學期望
- 定義:E(Y|X=x)=∫y*g(y|x)dy
定義,套用,期望的剩餘方差,
定義
設X和Y是離散隨機變數,則X的條件期望在給定事件Y = y條件下是y的在Y的值域的函式
 條件期望函式
條件期望函式其中,是x處於X的值域。
如果現在X是一個連續隨機變數,而在Y仍然是一個離散變數,條件期望是:
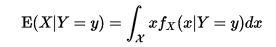 條件期望
條件期望其中,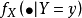 是在給定Y=y下X的條件機率密度函式。
是在給定Y=y下X的條件機率密度函式。
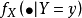
套用
條件數學期望在近代機率論中有著基本重要的作用,在實際問題中也有很大用處。在兩個互有影響的隨機變數中,如果已知其中一個隨機變數的取值=y,要據此去估計或預測另一個隨機變數的取值,這樣的問題在實際套用中經常會碰到。人們稱它為“預測問題”。由上述討論可知,條件數學期望E( )是在已知(=y)發生的條件下,對 的一個頗為“合理”的預測。
一般認為,人的身高和腳印長可當作一個二維常態分配變數來處理。
E( x,y) 或{x,E( x)}
可以得到平面上的兩條曲線,它們稱為是回歸曲線或簡稱為回歸。
期望的剩餘方差
還有一點應該指出的是,對於用得最廣泛的常態分配來說,可以從例3.27知道,兩類回歸恰好是一致的。這一事實表明,就常態分配而言,最佳線性估計就是最佳估計。當然,這裡“最佳”的意思是指均方差最小

