基本介紹
- 中文名:格點分布
- 外文名:lattice distribution
- 所屬學科:數學
- 別名:格子點分布、算術分布等
- 所屬問題:機率論與統計學
- 定義:一類離散型機率分布
定義









圓格點分布

相關定理
費勒(FelIer)初等更新定理




布萊克韋爾(Blackwell)更新定理













交錯更新過程













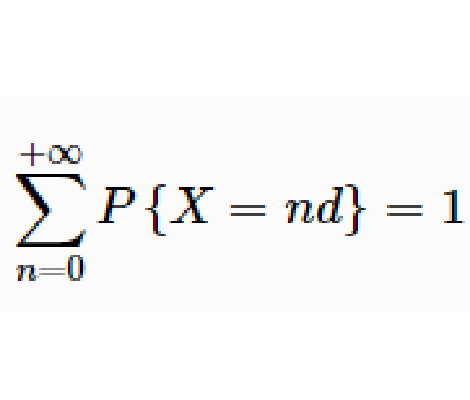








































格點分布亦稱算術分布,是指一類離散型機率分布。稱隨機變數服從算術分布,如果其一切可能值構成(有限或無限)等差數列,即其一切可能值可以表示為a±md(m=0,1,2,…)的形式,其中a和d為常數;d稱做分布的“步長”。二項...
離散圓周均勻分布 離散圓周均勻分布亦稱均勻闕周格點分布。圓周上的離散均勻分布。
由Atiyah-singer指標定理,格點上的拓撲荷密度也可由Overlap-Dirac算符求跡而得到,我們比較研究了用不同方法得到的拓撲荷,拓撲荷密度,拓撲感應率等等。 我們用各向異性的點陣和場論定義研究了淬火近似下有限溫度格點QCD的拓撲荷分布,拓撲...
《格點規範理論的解析研究》是依託四川大學,由鄭希特擔任項目負責人的面上項目。 項目摘要 探索了粉碎腎結石引起血尿等有關機理,關鍵是:(1)焦點對準結石;(2)使脈衝負壓適當;(3)相對抑制脈衝低頻成分,藉以適當減少空化、改善...
如果把全球每一個經緯度算作一個格點,沿著緯線是360個格點,沿著經線是180個格點,垂直方向大氣也是運動的,考慮50層,也就是50個格點。這樣,描述全球大氣運動需要格點的數量級為10⁶到10⁷。但是,遠遠做不到全球這些格點上都有...
布喇菲格子的格點,可以看成分列在相互平行、間距相等的平面繫上,而無遺漏,這些包含格點的平面稱為晶面。因為空間格子是概括地表明晶體結構中等同點的幾何圖形,所以任何晶面必然要平行空間格子的一個格點平面。根據周期性,任何格點平面都...
我們考慮的隨機環境主要是完全圖、格點或齊次樹上的獨立同分布隨機邊權重或獨立同分布隨機點權重的情形。其中,當邊(點)權重的分布取兩點分布這一特殊情形時,隨機環境就轉化為完全圖上的Erdos-Renyi模型、格點上的邊(點)滲流模型、子代...
GRIB是WMO開發的一種用於交換和存儲規則分布數據的二進制檔案格式。最初GRIB表示“二進制格點”(GRIdded Binary),後來擴展為“二進制的通用規則分布信息”(General Regularly-distributed Information in Binary form)。目前有兩個版本,...
按結構形式分類,有規則格點(格網)數字地面模型,散點數字地面模型、等值線數字地而模型、曲面數字地面模型、線路數字地面模型、平面多邊形數字地面模型和空間多邊形數字地面模型等七類,其中空間多邊形數字地面模型又可細分為坡元數字地面模型...
面心晶格又稱面心點陣。是指在當平行六面體晶格單位中,除在原有格點(即點陣點)外,另在平行六面體二處面心位置亦有格點,因此,正當面心晶格單位包含斗個格點、 與4個索晶格單位相對應。只有方晶系和交晶系中有面心晶格這種止當...
然後按自西向東的格點層次連線像點和按低緯向高緯的格點層次連線像點,並進行隱線消除。從而使原二維天氣圖上的等壓線,轉換成高低起伏的曲面,即一幅鳥瞰的三維500hPa等壓面,以曲面的谷峰表示等壓面的槽脊。技術要點 (1)成像原理 顯...
我們假設隨機向量列{(Zn,Yn),n≥1}是獨立同分布的,從而{Zn),{Yn}都是獨立同分布的,即Zi,Yi在i≠j時獨立,但Zi,Yi允許不獨立.下面利用關鍵更新定理得到交替更新過程的一個很重要的結論.定理:設H是Zn的分布,G是Yn的...
例如,關於素數定理,即不大於x的素數個數π(x)等於多少的問題(見素數分布)。此外,利用分析概念還可提出新的數論問題,例如各種數論函式的階估計及均值估計(見格點問題)。解決一個數論問題需要用到多深的分析工具,或者能否不用分析...
