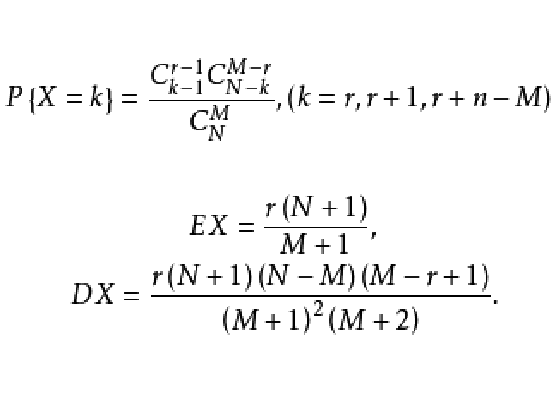負超幾何分布(negative hypergeometric distribution)是一種離散型分布。指自有限總體接連進行非還原抽樣直到具有特徵A的元素恰好出現r次為止，所需抽樣次數X服從參數為(r，N，M)的負超幾何分布，其中N是總體中元素的總數，M是具有特徵A的元素的個數。
基本介紹
- 中文名：負超幾何分布
- 外文名：negative hypergeometric distribution
- 所屬學科：數學
- 所屬問題：排列組合
- 別名：逆超幾何分布
- 性質：非還原抽樣次數的分布
定義,基本介紹,例題解析,
定義
負超幾何分布，亦稱逆超幾何分布，是非還原抽樣次數的分布。假如總體
含
個元素，其中
個具有特徵
；陸續自 非還原地一個一個地抽取元素，直到恰好出現
個具有特徵
的元素為止，則所需抽樣的次數
服從參數為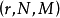
的負超幾何分布，此分布用於抽樣問題。
基本介紹
例題解析
例1 在一盒子裡有
把鑰匙，其中有
把是對應
個箱子的，其餘
把是房間的鑰匙，每次隨機地從盒子裡抽取一把鑰匙，且取後不放回，若取到直至第
個箱子打開為止，這時一共取出了
把鑰匙，若盒子裡的每把鑰匙有相同的機會被取到，求
的分布?
解：事件“
”等價於“在前
把鑰匙中有
把是箱子的鑰匙，且最後一次取出的鑰匙是箱子的”。由於鑰匙取出後不再放回，故有
(前
把鑰匙中有 把是箱子的)
(從
把房間鑰匙、
把箱子鑰匙中取出一把箱子鑰匙)
