基本介紹
- 中文名:柏拉圖多面體
- 第一條:簡介
- 第二條:多面體
- 第三條:證明
簡介,多面體,證明,關係,
簡介
熟悉柏拉圖多面體的最佳方法莫過於經由構造模型並透過模型研究它們。下圖表示一種稱之為“展開圖”的個別柏拉圖多面體平面排列圖示。為了構造柏拉圖多面體的模型,一組類似的展開圖必須被描繪在適當的材料上。同學可以將本資料所附之多面體的展開圖直接剪下或經放大、縮小影印在合適的漂亮紙張上。如果材料不方便影印,您也可以依樣繪製或把影印展開圖並貼在所用材料上。Albrecht Durei早在1525年,於他所著的《Unterweisung der Messung Mit dem Zirkel und Richtsheit》一書中,給出了幾個多面體的展開圖。
多面體
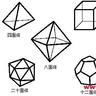
很容易看出柏拉圖多面體每一個都是凸的,並且在每一個頂點處交會著相同數目、相似、正的凸多邊形。要理解為什麼只有五個柏拉圖多面體是相當簡單的,這是因為在每一個頂點處交會著至少三個面才能構造出一個立體圖形,而且圍繞每一個頂點的面的角度和不能等於或超過360°,否則所得的面將是平的或是凹的。
具有最少邊數的正多邊形是正三角形,三個如此的多邊形可以使它們交會在一個頂點上,接下來,加入第四個面,如此,每三個面就會交會在圖形的四個頂點處之一。由於這個圖形有四個全等的面,故稱之為正四面體(TETRAHEDRON)。
四個正三角形可以使它們交會在一個頂點上,而且加入四個面之後,在圖形的六個頂點處都會有四個面交會在這裡。由於這個圖形有八個面,故稱之為正八面體(OCTAHEDRON)。
另外,我們可以構造出五個正三角形可以交會在它的12個頂點處的圖形。由於這樣的圖形有20個面。故稱之為正二十面體。
假如六個正三角形交會在一頂點處,那么交會在這頂點的面的角之總和為360°,於是這些三角形將構成一平面。所以表面是正三角形的柏拉圖多面體只能有三種。
接下來要考慮的多邊形是正方形,我們可以構造成三個正方形交會在它的八個頂點處的多面體,它是另一種柏拉圖多面體,一般稱之為正方立體(CUBE),由於它有六個面,故亦稱之為正六面體(HEXAHEDRON)。
一個凸多面體不能由每個頂點處都有四個正方形交會,這是由於交會在每個頂點處的面的角之總和將會是360°。
接下來考慮的是有五個等邊及五個內角均是108°的正五邊形。一個多面體可以由三個交會在它的20個頂點處的正五邊形所構成所得的圖形稱之為正十二面體(DODECAHEDRON),這是由於它有12個面的緣故。通常我們也將其稱之為正五角十二面體。
四個五邊形將不能交會在一頂點而構成一凸多面體,這是由於這些交會在一頂點的面的角之總和將超過360°
接下來考慮的是正六邊形,但是假如三個正六邊形交會在一頂點處那么這些面的角之總和將是360°,於是構成一平面。從這裡也可以看出多邊形的面數愈多,它們的內角就愈大,多於六邊的正多邊形其三個內角之總和將超過360°,於是,無法將它們連線在一起而構成一正的凸多面體。
證明
假設一個正多面體共有 V 個頂點、F 塊面及 E 條邊;每一塊面均為正 n 邊形,且每一個頂點共有 m 塊面的頂點相連。
由於共有 F 塊面,且每塊面均為正 n 邊形,所以將該正多面體拆開為 F 個正 n 邊形後,應有 nF 條邊;
由於一個頂點與其他 m 個頂點相連,所以將該正多面體拆開為 F 個正 n 邊形後,應有 mV 個頂點,因多邊形頂點數目和邊的數目相等,即共有 mV 條邊;
同樣地,當多個正 n 邊形合成為一個正多面體時,兩個正 n 邊形的各一條邊便會合併成正多面體的一條邊,所以將該正多面體拆開後,應有 2E 條邊;
因此,可得 nF = mV = 2E
利用歐拉公式 V + F - E = 2
代入 V 及 F 得
重整後得
因 E 須為正整數(m - 2)(n - 2) < 4
因著基本立體幾何及平面幾何,m > 2 及 n > 2,所以 (m, n) 只可能為(3, 3)、(3, 4)、(4, 3)、(3, 5) 及(5, 3);即(V, F, E) 只可能為(4, 4, 6)、(8, 6, 12)、(6, 8, 12)、(20, 12, 30) 及(12, 20, 30)。
關係
柏拉圖視“四古典元素”為元素,其形狀如正多面體中的其中四個。
- 火的熱令人感到尖銳和刺痛,好像小小的正四面體。
- 空氣是用正八面體制的,可以粗略感受到,它極細小的結合體十分順滑。
- 當水放到人的手上,它會自然流出,那它就應該是由很多小球所組成,好像正二十面體。
- 土與其他的元素相異,因為它可以被堆疊,正如立方體。
剩下沒有用的正多面體——正十二面體,柏拉圖以不清晰的語調寫:“神使用正十二面體以整理整個天空旳星座。”柏拉圖的學生亞里士多德添加了第五個元素——以太(希臘文:Αιθήρ,拉丁轉寫:aithêr;拉丁文:aether),並認為天空是用此組成,但他沒有將以太和正十二面體連繫。
約翰內斯·克卜勒依隨文藝復興建立數學對應的傳統,將五個正多面體對應五個行星——水星、金星、火星、木星和土星,同時它們本身亦對應了五個古典元素。