五次對稱性是指,繞對稱軸旋轉2π/5角度後,恢復自身的對稱性。
定義
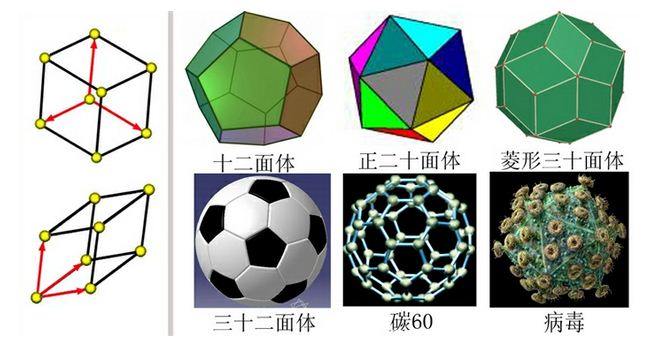 現在人們陸續發現的正多面體
現在人們陸續發現的正多面體五次對稱性是指,繞對稱軸旋轉2π/5角度後,恢復自身的對稱性。
 現在人們陸續發現的正多面體
現在人們陸續發現的正多面體五次對稱性是指,繞對稱軸旋轉2π/5角度後,恢復自身的對稱性。...... 五次對稱性是指,繞對稱軸旋轉2π/5角度後,恢復自身的對稱性。目錄 1 定義 2 晶體中的...
作者說,在古代的裝飾圖案中,尤其是古埃及的裝飾物中,能夠找到所有17種對稱性...這一論述非常關鍵,阿拉伯裝飾藝術的確時常費力地嘗試使用五次旋轉對稱。連續裝飾...
例如一個五角星,繞其中心軸旋轉,每轉動72º,與原來位置的圖形完全重合,就象未轉動一樣,因為每轉動360º能重合五次,因此稱五角星具有五次旋轉對稱性。由這個...
材料性能:各向異性對稱性與結構,作者是羅伯特·E·紐納姆,出版社於西安交通大學...詞條統計 瀏覽次數:次 編輯次數:5次歷史版本 最近更新: 創建者:yanlis猜...
5.美元日元的時間對稱關係6.歐元美元的時間對稱關係7.現貨黃金的時間對稱關係8.玉米連續的時間對稱關係9.上證指數本次上漲行情對稱性10.招商輪船的日線時間對稱關係...
4.恒生指數的時間對稱關係5.美元日元的時間對稱關係6.歐元美元的時間對稱關係7.現貨黃金的時間對稱關係8.玉米連續的時間對稱關係9.上證指數本次上漲行情對稱性...
準晶是具有準周期平移格子構造的固體,其中的原子常呈定向有序排列,但不作周期性平移重複,其對稱要素包含與晶體空間格子不相容的對稱。衍射花樣具有五次、八次、十次...
葉恆強與中國國外同時獨立地發現傳統晶體學不允許的五次對稱性,進而發現並研究了二十面體對稱、八次、立方對稱等準晶相。葉恆強在中國國內率先用高分辨原子象對固體...
普通晶體具有的是二次、三次、四次或六次旋轉對稱性,但是準晶的布拉格衍射圖具有其他的對稱性,例如五次對稱性或者更高的六次以上對稱性。 [1] ...
