基本介紹
- 中文名:有限小數
- 外文名:Finite number
- 解釋:小數點後的小數個數有限
- 基本性質:末尾添上零或去掉零小數不變
- 學科:數學
- 類別:小數
基本內容,讀法,大小比較,有限小數條件,相關計算,教學套用,
基本內容
十進制計數法:10個一是十,10個十是百……10個一百億是一千億,每相鄰兩個計數單位之間的進率都是十。這種計數方法叫做十進制計數法。
在測量物體時,往往會得到不是整數的數。於是古人就發明了小數來補充整數。小數是十進分數的一種特殊表現形式。小數可以分為有限小數、無限小數兩類,而無限小數又分無限循環小數與無限不循環小數兩類。 所有分數都可以表示成小數,小數中除無限不循環小數(無理數)外,都可以表示成分數。
小數中的圓點叫做小數點,它是一個小數的整數部分和小數部分的分界線,小數點左邊的部分是整數部分,小數點右邊的部分則是小數部分。整數部分為零的小數叫做純小數,而整數部分不是零的小數叫做帶小數。例如:0.3是純小數,3.1則是帶小數。
小數的基本性質是:在小數的末尾添上零或去掉零,小數的大小不變。
讀法
小數的讀法有兩種:一種是按照分數的讀法來讀。帶小數的整數部分按整數讀法讀;小數部分按分數讀法讀。例如:0.38讀作“百分之三十八”,14.56讀作“十四又百分之五十六”。另一種讀法是:整數部分仍按整數的讀法來讀,小數點讀作“點”,小數部分順次讀出每個數位上的數字。例如:0.45讀作“零點四五”;56.032讀作“五十六點零三二”。
大小比較
同整數一樣,小數的計數單位也按照一定的順序排列起來,它們所占的位置叫做小數的數位。數位順序為十分位、百分位、千分位、萬分位、十萬分位、百萬分位……。
小數的大小比較:先看整數部分,整數部分較大的,這個數就大;整數部分相同就看十分位,十分位較大的,這個數就大;十分位相同就看百分位,百分位較大的,這個數就大。以此類推。
把小數點分別向右移動一位、二位、三位……,小數的值就分別相應擴大到原數的10倍、100倍、1000倍……。把小數點分別向左移動一位、二位、三位……,小數的值就分別相應縮小到原數的十分之一、 百分之一、 千分之一……。例如,要把7.4擴大到原數的10倍,只需將7.4的小數點向右移動一位,即74;若要把3.08縮小到原數的百分之一,只需將3.08的小數點向左移動2位,即0.0308(注意,當小數的位數不夠時,需在前面加上相應個“0”)。
有限小數條件
能寫作兩個整數的比的數叫做有理數。整數和通常所說的分數都是有理數.有理數可以劃分為正有理數、0和負有理數。如3,-98.11,5.72727272……,7/22等,都是有理數。在數的十進制小數表示系統中,有理數就是可表示為有限小數或無限循環小數的數。這一定義在其他進位制下(如二進制)也適用。
一個最簡分數,如果分母中除了2和5以外,不含有其他的質因數,這個分數就能化成有限小數;如果分母中含有2和5以外的質因數,這個分數就不能化成有限小數。即最簡分數a/b能化為有限小數的充要條件是分母b不含有2和5以外的質因數。
相關計算
例1:判別下面各分數,哪些能化成有限小數,哪些不能化成有限小數?

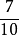

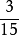

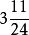
教學套用
在教學過程中,讓學生經歷探究過程,一方面有助於學生掌握新知。數學學習過程蘊藏著比知識更具有智力價值的數學思想與方法。在教學中,教師應該重視學生的學習過程,充分尊重了學生的認識水平和已有知識經驗。讓學生先是通過計算把分數化成小數( 除不盡的保留三位小數),再把這些分數根據是否能化成有限小數分成兩類。然後引導學生觀察比較,能夠化成有限小數的分數的秘密。促使學生大膽進行猜想,並進行驗證。這樣,給學生提供了自主探究空間與時間。 在驗證自己猜想的過程中,學生的思維活躍,可以通過認真觀察,獨立思考,發現秘密是在分數的分母。再將分母分解質因數,發現了分母分解出來的質因數只含有2與5。在整個探究過程中,充分調動學生學習的積極性與主動性,經歷知識探究過程,學生髮現並理解所學的知識,從而也掌握了一種“猜想—驗證”的學習方法。

