基本介紹
- 中文名:最小正周期
- 外文名:minimal positive period
- 領域:數學
- 算法實例:函式f(x)±g(x)最小正周期的求法
- 基本概念:函式f(x)所有周期中最小的正數
- 套用:圖像分析、信號處理
算法實例
定義法




公式法
最低公倍數法
圖象法






恆等變換法



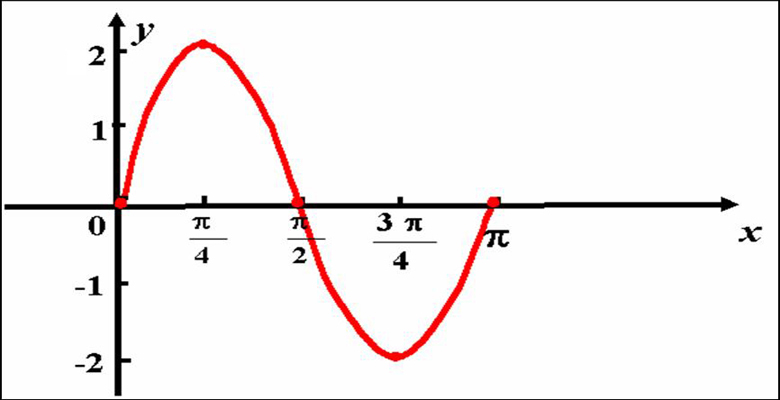













如果一個函式f(x)的所有周期中存在一個最小的正數,那么這個最小的正數就叫做f(x)的最小正周期(minimal positive period).例如,正弦函式的最小正周期是2π....
若f(x)是在集M上以T*為最小正周期的周期函式,則K f(x)+C(K≠0)和1/ f(x)分別是集M和集{X/ f(x) ≠0,X ∈M}上的以T*為最小正周期的周期...
最小正周期:kπ,k∈Z單調性:有單調增區間:(-π/2+kπ,+π/2+kπ),k∈Z單調減區間:無正切特殊角 編輯 tan15° 2-√3 tan30° √3/3 tan45° 1...
正割(Secant,sec)是三角函式的一種。它的定義域不是整個實數集,值域是絕對值大於等於一的實數。它是周期函式,其最小正周期為2π。正割是三角函式的正函式(正弦...
餘切函式的圖象由一些隔離的分支組成(如圖)。餘切函式是無界函式,可取一切實數值,也是奇函式和周期函式,其最小正周期是π [2] 。...
5、周期性:最小正周期π(可用π/|ω|來求) 6、最值:無最大值與最小值 7、零點:kπ,k∈Z 8、對稱性:軸對稱:無對稱軸 中心對稱:關於點(kπ/2,0)對...
最小正周期:2πsin函式奇偶性 奇函式 (其圖象關於原點對稱)sin函式單調性 在[-(π/2)+2kπ,(π/2)+2kπ],k∈Z上是增函式...
在這種方式下,正弦和餘弦變成了周期為 2π的周期函式:對於任何角度θ和任何整數k。周期函式的最小正周期叫做這個函式的“基本周期”。正弦、餘弦、正割或餘割的...
求分段函式的最小正周期的方法有:定義法、公式法和作圖法。例6 求函式f(x)= 的最小正周期。定義法:當x=2kπ或2kπ+π時,sin(2kπ+π)=sin2kπ=0...
5、周期性:最小正周期為2π。 6、奇偶性:奇函式。 7、圖像漸近線:x=kπ,k∈Z餘割函式與正弦函式互為倒數)。[2] 圖像 圖3.餘割函式圖像 套用 正弦律...
