最嚴謹檢驗亦稱最緊迫檢驗,是指功效與一切可能檢驗的最大功效之絕對差最小的檢驗。
基本介紹
- 中文名:最嚴謹檢驗
- 外文名:most strict test
- 所屬學科:數學
- 所屬問題:統計學(檢驗假設)
- 別名:最緊迫檢驗
基本介紹
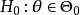
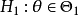

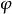
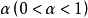

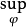
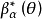
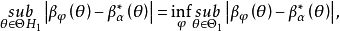
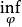
無偏方差

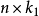
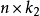
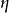
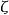
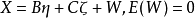
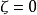
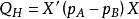
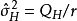
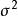
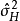
線性假設的標準型
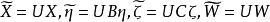
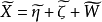
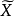
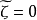

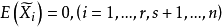
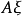
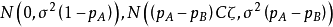
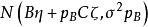

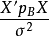
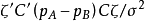
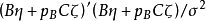
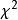
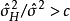
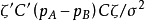
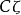

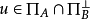
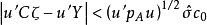
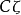
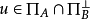
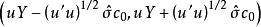
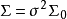

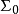
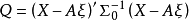
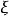
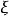
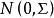
因素 | 平方和 | 自由度 | 均 方 |
HB誤差 | 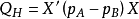 | r |  |
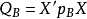 | s-r | 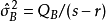 | |
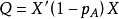 | n-s | 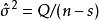 | |
總和 | 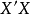 | n |
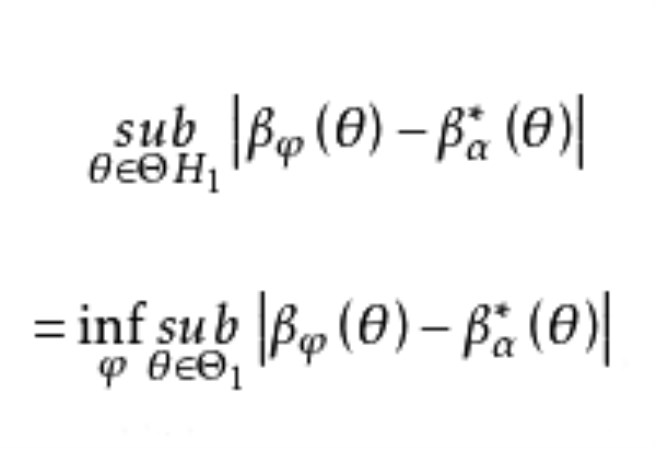
最嚴謹檢驗亦稱最緊迫檢驗,是指功效與一切可能檢驗的最大功效之絕對差最小的檢驗。
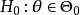
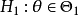

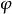
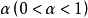

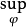
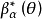
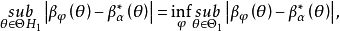
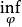

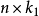
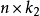
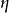
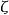
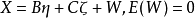
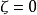
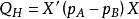
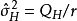
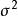
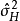
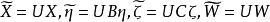
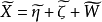
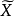
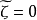

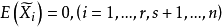
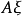
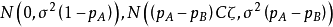
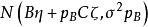

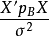
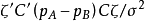
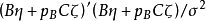
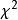
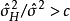
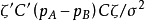
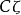

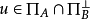
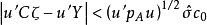
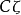
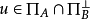
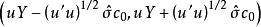
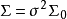

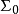
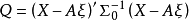
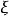
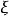
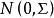
因素 | 平方和 | 自由度 | 均 方 |
HB誤差 | 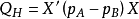 | r |  |
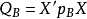 | s-r | 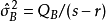 | |
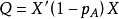 | n-s | 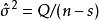 | |
總和 | 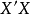 | n |
最嚴謹檢驗亦稱最緊迫檢驗,是指功效與一切可能檢驗的最大功效之絕對差最小的檢驗。...... 最嚴謹檢驗亦稱最緊迫檢驗,是指功效與一切可能檢驗的最大功效之絕對差最...
學術嚴謹性檢驗,即從學術的角度嚴謹地思考戰略的原創性、思維的邏輯性和方法的科學性。優秀的戰略在於其原創性。但是,在實踐中要特別注意把握創新的程度,因為過度的...
① 抽樣嚴謹抽樣檢驗是一個統計學機率存在風險,這種風險可能把不良品漏檢而放到生產線上去,也可能把合格品判退,從而間接造成本公司的損失,所以在抽樣時,一定要盡...
若要更為嚴謹的話,可以採用微分檢驗法。中文名 積分檢驗法 外文名 Integral ...活度係數是最便於聯繫T、p、x、y值的,採用Gibbs-Duhem方程的活度係數形式來...
“公正、嚴謹、專業、高效”的服務為使命,近400名專業的技術人員可為客戶提供一...將CCIC福建公司打造成海峽西岸經濟區最專業、最具有品牌影響力的綜合型檢驗認證...
中心擁有一支強大的技術專家團隊,憑藉在電線電纜產品檢驗和標準研究領域豐富的專業知識和技術積累,為電線電纜製造企業提供嚴謹、專注的產品檢驗及技術服務。 中心的實驗...
食品檢驗是食品安全監管最權威、最嚴謹的技術支撐,食品是否合格和安全,要通過食品檢驗來驗證。各食品安全監管部門要高度重視食品安全抽樣檢驗工作,嚴把食品檢驗關口,...
秉承專業化、獨立、及時、高效的企業精神,以嚴謹的態度,高度的責任感。...進行檢驗或者實驗見證,從而規避產品批量的產生問題,同時最大限度的減低產品在成品...
培訓”為主業的跨國檢驗認證機構,是目前國內最大型的檢驗認證機構,獲得客戶以及...以公平公正的態度和科學嚴謹的精神執行每一項工作,藉助集團公司全球網路,為您提供...
他們的工作以最終檢驗為主,在出貨前把關。驗貨員的工作就是嚴謹、仔細的檢查產品質量,客觀、公正的反應產品質量情況,並如實填寫驗貨報告。...
民以食為天、食以安為先。習近平總書記在去年底召開的中央農村工作會議上強調,用“最嚴謹的標準、最嚴格的監管、最嚴厲的處罰、最嚴肅的問責”,確保廣大人民民眾“...
