換元法

概述

亦稱輔助未知數法，又稱變元代換法.解方程組的一種重要方法。它是普遍套用的一種方法，其一般意義是將由一個或幾個變元構成的數學表達式中的一部分用新的變元表示，以利於問題的解決.這裡僅給出在解方程(組)和解不等式(組)中的套用。

它可以化高次為低次、化分式為整式、化無理式為有理式、化超越式為代數式，在研究方程、不等式、函式、數列、三角等問題中有廣泛的套用。

換元法是指引入一個或幾個新的變數代替原來的某些變數的變數求出結果之後，返回去求原變數的結果.換元法通過引入新的元素將分散的條件聯繫起來，或者把隱含的條件顯示出來，或者把條件與結論聯繫起來，或者變為熟悉的問題.其理論根據是等量代換.

高中數學中換元法主要有以下兩類：

(1)整體換元：以“元”換“式”。

(2)三角換元，以“式”換“元”。

(3)此外，還有對稱換元、均值換元、萬能換元等.換元法套用比較廣泛。如解方程，解不等式，證明不等式，求函式的值域，求數列的通項與和等，另外在解析幾何中也有廣泛的套用。

我們使用換元法時，要遵循有利於運算、有利於標準化的原則，換元後要注重新變數範圍的選取，一定要使新變數取值範圍對應於原變數的取值範圍，不能縮小也不能擴大。如上幾例中的t>0和sinα∈[-1,1 ]。

可以先觀察算式，可發現這種需換元法之算式中總含有相同的式子，然後把它們用一個字母替換，推演出答案，然後若在答案中有此字母，即將該式帶入其中，遂可算出。

有時在分解因式時，可以選擇多項式中的相同的部分換成另一個未知數，然後進行因式分解，最後再轉換回來，這種方法叫做換元法。

注意:換元後勿忘還元。

【例】在分解(x²+x+1)(x²+x+2)-12時，可以令y=x²+x,則　原式=(y+1)(y+2)-12　=y²+3y+2-12=y²+3y-10　=(y+5)(y-2)　=(x²+x+5)(x²+x-2)　=(x²+x+5)(x+2)(x-1)．

例2，(x+5)+(y-4)=8

(x+5)-(y-4)=4

令x+5=m,y-4=n

原方程可寫為

解得m=6,n=2

所以x+5=6,y-4=2

所以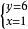

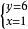
特點：兩方程中都含有相同的代數式，如題中的x+5,y-4之類，換元後可簡化方程。

解高次方程

有時在解方程時，可以選擇方程中的相同的部分換成另一個未知數，達到降次的目的，然後進行新方程求新未知數，最後再轉換回來求原未知數，這種方法叫做換元法。