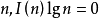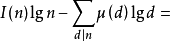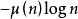曼戈爾特函式

曼戈爾特函式(von Mangoldt function)是曼戈爾特提出來的以他的名字命名的函式，也稱第二切比雪夫函式，它在素數分布論中有重要作用。曼戈爾特函式記為Λ(n)。

基本介紹

• 中文名：曼戈爾特函式
• 外文名：von Mangoldt function
• 提出者：曼戈爾特
• 別稱：第二切比雪夫函式
• 符號：Λ(n)
• 相關概念：素數定理、麥比烏斯反演公式等

定義

對每一個整數 ，我們定義

是的牟比烏斯變換，而是的牟比烏斯變換。切比曉夫證明了若成立則素數定理成立。

為了便於理解，我們將 的值列於簡表1中。

表1

	1	2	3	4	5	6	7	8	9	10

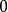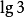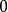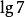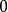相關定理

對於曼戈爾特函式我們有如下定理．

定理1 如果，我們有

定理2 設為整數，且，則有

證明： 對式(1)用麥比烏斯反演公式，因為對所有的正整數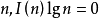，因此可得

曼戈爾特

曼戈爾特(Hans Carl Friedrich von Mangoldt，1854-1925)是一位德國數學家，生於魏瑪。卒于波蘭的但澤(Danzig)，1884年在漢諾瓦(Hannover)成為數學教授，先後執教於亞琛(1886)和但澤(1904)，曼戈爾特專門研究數論，特別對素數定理有重要貢獻，他提出了以其名字命名的曼戈爾特函式，它在素數分布論中有重要作用。