運動的光源與觀測者之間不但會發生都卜勒效應，同時還會發生時間效應，其物理性質、數學形式完全相同，如同一個金幣的正面與反面。進一步推演出；超光速天體，與在盲區，觀察中；天體倒自行，並時間觀測倒流。
基本介紹
關鍵字,引言,時差方程,討論與結論,超光速天體,退行的星系,可測距離,實驗報告,解題,
關鍵字
時差方程、觀測真時、被測真時、本鐘、盲區、倒自行
引言
本文探討結果；空間處處時間流程相同，時鐘測下的時間、都為空間標準真時間。但；存在相互運動的坐標系之間，測者測下被測坐標系內的事件的時間，不為被測事件的真時間，即不為被測坐標系內的真時間，必須把觀測時間轉換成被測時間，因相互運動的坐標系之間發生了——時間效應，其效應的物理性質與都卜勒效應物理性質完全相同。
都卜勒效應已為實踐所證明與套用，時間效應同樣能做實驗，其實驗方法與都卜勒效應實驗方法完全相同。
時差方程
空間一參照系S。，在原點O。上有一靜止測者與一時鐘，在S。系坐標P1、P2點上各有一靜止點光源與一時鐘，把這三鐘同步。通過O。、P1、P2三個點可以做一個平面，P1、P2連線在該平面內，O。點至P1、P2連線的垂線長為ρ 。通過P2、 O。、X1三個點可以做另一個平面，X。軸在該平面內，P2至X。軸的垂線長為ρ'，見圖<1>：
P1、P2點上的點光源，在同一瞬間，各自發射了一個脈衝光訊號，即它們的時間間隔T。=O ，二個光訊號是同時發射的，而在O。點上的測者卻不是在同一瞬間同時接收到二個光訊號。由圖<1>知道
P1O。<P2O。，故，觀測時間 t′≠ 0 、t′≠ T。
光訊號；由P傳送到O。的時間為t1，由P2傳送到O。的時間為t2，那么觀測時間t′與被測時間T。的關係為；t1與t2的差值：
即 T。- t′= t1 - t2
移項得 t′= T。- (t1 - t2) <1-1>
<1－1>式為時差方程。
現有一慣性系S，以U。速率沿P1、P2連線運動，在S系原點O上有一靜止於S系的光源與時鐘，當S系原點O到達P1點的瞬間；P1點與O點上的光源，在同一瞬間各自發射了一個脈衝光訊號，二個光訊號經過t′時間間隔，在同一瞬間到達O。(由光性質知道，光速為常數C。，與光源有無運動無關)，也就是O。點上的測者在同一瞬間同時接收到了這二個光訊號。當原點O到達P2的瞬間，P2點與O點上的光源也同步各自發射了一個光訊號，經過t2時間間隔在同一瞬間到達O。點，O。點上的測者根據時鐘記錄，觀測時間為t′，由P1、P2點上時鐘記錄知道，S系由P1到達P2的時間間隔為T。(S繫上的時鐘測下時間間隔是否為T。，後面再討論)。
解方程：
將時差方程兩邊除以T。
得： t′/T。= 1－(t1－t2)/T。 <1－2>
由圖<1>得：
t1=ρ/sinαc。 t2=ρ/sinα′c。
T。=(1/tgα-1/tgα′)ρ/U。代入<1－2>式得：
t′/T。=1－(ρ/sinαc。-ρ/sinα′c。)/(1/tgα-1/tgα′)ρ/U。
整理得：
t′/T。=1－U。(sinα′－sinα)/C。sin(α′－α)
將α′=α+θ 代入上式，
整理得：
t′=T。{1-(U。/C。)[cosα-sinα(1-cosθ)^1/2/(1+cosθ)^1/2]} <1－3>
<1-3>式為光源(運動)與測者(靜止)之間的觀測時間效應式。
Lim[sinα(1-cosθ)^1/2/(1+cosθ)^1/2]=0
θ－>0
得： t′ = T。( 1 - Cos α U。 / C。) <1-4>
我們知道<1-4>式是觀測時間效應<1-3>式的極限形式。
如果S系的光源,在T。時間內發射了f個短脈衝光訊號,那么S。系的測者,在t′時間內接收了f個脈衝光訊號。S系的光源發射頻率為ν。= f / T。,而S。系的測者,接收頻率為ν′ = f / t′ ,將f 除以<1-4>式兩邊得：
ν′ = ν。/ (1 - Cos α U。/ C。) <1-5>
如果S系的發射源是一個無線電發射源,那么它的發射波長為λ。= C。/ ν。,測者的接收波長為λ′ = C。/ν′將C。除以<1-5>式兩邊得：
λ′ = λ。( 1- Cos α U。/ C。) <1-6>
以上探討我們知道；時間效應與都卜勒效應其物理性質、數學形式完全相同。
在P2點上的光源,在t′ 時間間隔內發射了f (f = f1 + f2 + f3 + ┅ + fn )個光訊號,O。點上測者接收到f1的瞬間以V。的速率沿X。軸運動,到達X1的瞬間接收了第fn個光訊號,測者由O。點運動到X1,的時間間隔為t。,笫fn個光訊號由P2到達X1的時間間隔為T3 ,建立時差方程：
t′ - t。= t2 - t3 <1-7>
將<1-7>式移項,再除以 t。,得：
t′ / t。 = 1+ ( t2 - t3) / t。
將 t2 = ρ′ / Sin β C。 t3 = ρ′ / Sin β′ C。 t。 = ( 1 - / tg β - 1 / tg β′ ) ρ′ / V。 代入上式,其整理、解法與<1-2>式整理、解法同理,
得： t。 = t′ / ( 1 + Cos β V。 / C。 ) <1- 8 >
ν = ν′ ( 1 + Cos β V。 / C。 ) <1- 9 >
λ = λ′ /( 1 + Cos β V。 / C。 ) <1-10>
由<1-4>、<1-5>、<1-6>式知道；S系的發射源,原本由P1點運動到P2的時間間隔為T。,發射頻率為ν。,發射波長為λ。,由於時間、都卜勒效應的結果；使得T。為t′ 、ν。為 ν′ 、 λ。為 λ′ ,
將<1-4>、<1-5>、<1-6>式代入<1-8>、<1-9>、<1-10>式得：
t。 = T。( 1 - Cos α U。/ C。) / ( 1+ Cos β V。 / C。) <1-11>
ν = ν。( 1 + Cos β V。/ C。) / ( 1- Cos α U。 / C。) <1-12>
λ = λ。( 1 - Cos α U。/ C。) / ( 1+Cos β V。/ C。) <1-13>
由<1-11>與<1-13>式得：
T。= t。λ。/ λ <1-14>
討論與結論
作為計時器,經歷了機械鐘、石英鐘、原子鐘,原子鐘其精度為每30萬年誤差 1 秒。秒的物理量；1967年13屆國際計量大會定義為：絕133原子對應與兩個超精細能級躍遷9192631770個輻射周期的持續時間。而原子的能級躍遷所輻射的電磁波頻率異常穩定,其計時精度精確到每天1×10^-13秒,因此,原子鐘被用來測定標準時間,日常在電台、電視上的報時,就來自原子鐘^①。
原子鐘有精確穩定的"電磁頻率",故,有精確的計時,如果"電磁頻率"不穩定,快了,或慢了,那時鐘也會走快了,或走慢了,故,時鐘的"頻率"穩定至關重要！
一個穩定頻率的無線電磁波發射源,與一個電磁波接收計數器,構成一個計時系統,如果頻率穩定達到原子鐘級,可以作為標準時間計時器。但,當它們之間存在相互運動時,大家知道；就會發生都卜勒效應,也就是接收頻率發生了變化；當它們相互靠近運動時,頻率變高了,計時系統計時變快了(時鐘變快了),當它們相互背離運動時,頻率變低了,計時系統計時變慢了(時鐘變慢了)。
都卜勒效應可以做實驗,用頻率計測定標準頻率發射台(我國的授時中心BPM台,頻率有2.5MHZ、5MHZ、10MHZ、15MHZ),在發射10MHZ時段,相對發射台靜止時,測下頻率為10MHZ,那么測定的周期為100納秒,當向著電台運動時,測下的頻率大於10MHZ,也就是測定的周期小於100納秒,當背離電台運動時,測下的頻率小於10MHZ,測定的周期大於100納秒。
頻率的倒數是周期,周期就是時間,所以；發生都卜勒效應,必定發生時間效應,時間效應與都卜勒效應是同時發,兩者不可分割!
我們得出結論①：時向間效應與都卜勒效應同屬於一個物理性質,發生都卜勒效應,必然發生時間效應,時、頻效應是同時發生的,不可分割的,如同一個金幣的正面與反面。
由上一節探討知道,發射源與測者之間存在相互運動時,發生了時、頻效應,見圖<2>：以測者所在坐標S係為參考系，以發射源運動方向為X軸方向，以發射源運動連線的垂線為Z軸(測者天頂)，發射源相對S系由P向P′以U的速率運動。發射源在運動過程，電磁波由發射源到達測者的路程，是在不斷的改變時，而發生時、頻效應。
結論(2)：當電磁波以不同路程由發射源到達測者時就會發生——時、頻效應。
由圖中還知道，發射源相對測者的運動速率分量角，除之0與π外，也就是發射源正向著測者或正背離測者作勻速運動時，觀測頻率是不變的，除此之外，不管發射源是靠近測者或是背離測者運動的，分量角(由α向α′過渡)都在漸漸變大。也就是測者的觀測頻率；由高漸漸變低，頻率的倒數是周期(也就是將1除以<1-5>式兩邊，得出的就是<1-4>式)，觀測周期在漸漸變慢。
結論(3)：測者在觀測過程，發生了時、頻效應，不管發射源是向著測者或是背離測者運動；其觀測周期都在漸漸變慢。
結論③的觀測周期在漸漸變慢，與脈衝星觀測周期在漸漸變慢，可有圖<2>與<1-6>式知道，可以驗證；只要檢查年自值較大天體的早年所攝的光譜線，與現近所攝的光譜線作比較，紫移效應的天體；視速率在漸漸變慢，紅移效應的天體；視速率在漸漸變快！
在上我們已探討到;發射源的運動速率分量角為0、或為π時,觀測頻率是不變的,由都卜勒效應所觀測的速率為運動源的真速率！除分量角為0與π之外;而所觀測的速率並不為被觀測的運動源的真速率;僅為視速率！如圖<2>中,運動源運動到z軸位置時,o點位置的觀測者,觀測視速率為0,那怕是幾倍光速運動的天體[紅移z值大於1的類星體,視速率已大於光速(λ/λ。=(λ。+Δλ)/λ。=1+z)]ˆ③,視速率仍為0！視速率為0的脈衝星,觀測視周期為真周期！
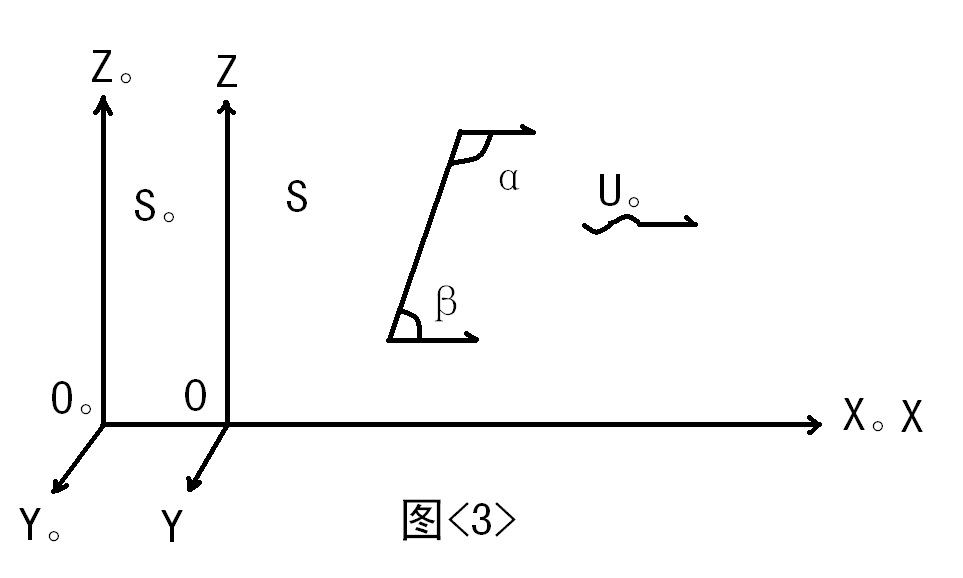
上面我們已探討過，一個頻率穩定的電磁波發射源與一個電磁波接收計數器，可以構成一個計時系統。該計時系統靜止於一慣性坐標系內，電磁波由發射源到達接收計數器的路程是不變的，故不會發生時、頻效應，該系統記錄的時間是標準時間。但；該慣性系不是靜止的，在空間相對一參照系作勻速直線運動的，見圖<3>：
從圖中我們知道，α=π -β U。=V。代入<1-11><1-12>式，結果得：t。=T。 ν=ν。，不會發生時、頻效應。實質上，在慣性內靜止的發射源與接收計數器，電磁波由發射源到達接收計數器的路程還是不變，故不會發生時、頻效應，該計時系統的時間記錄，還是標準時間，還為真時。我們得出；
結論(4)：一切慣性系內的時鐘，所記錄時間都為空間標準時間，都為真時，與慣性系有無運動無關。
但.非慣性系內的靜止電磁波發射源與電磁波接收器,電磁波由發射源到達接收器的路程；是在做微小的變化,我們在這裡只做定量簡單的分析,見圖<3-1>。S。與S兩坐標系;X。、X軸與X。Y。、XY平面而重合,電磁波發射源靜止予S系P點上,兩個電磁波接收器分別靜止予S系O點與S。系X。軸X′處。S系靜止予S。系時,光信號(電磁波信號)由P至O、X′的光時分別為t。與t (測得光程分別為L。與L , L。≠L),當P點上的發射源發射信號的瞬間;S系以U。速率沿X。軸運動,經過t時間間隔, 光信號由P點運動到X′點,此瞬間； O點也正到達X′點(O點運動了一段U。t 距離), 也就是；當S系以U。速率沿X。運動時,光信號由P點至O點的光時不再為t。,而為t ! 光程由L。變為L !
在運動慣性系內，靜止的發射源與接收器, 光信號由發射源至接收器的光程同為L,是不變的,與慣性系的運動無關，故不會發生時、頻效應。
如果發射源沿XY平面以L。為半徑繞O點做園周運動, 由圖<3-1>知θ。= 0時, 電磁波信號由P點至O點的光時
t = t。/(1+U。^2/C。^2 ), θ。= π/2 時, t=t。/(1-U。^2/C。^2)^1/2, θ。=π時, t=t。/(1-U。^2/C。^2) 。
t′=t。/[1+ (U。+ΔU′) ^2/C。^2], t″=t。/[1+(U。+ΔU′+ΔU″) ^2/C。^2], ……,
是否是,時、頻效應的結果,可以驗證；將三座同原子、同尺度、同結構的原子鐘,先將兩座鐘,並列在一起,同位子、同方向,另一鐘隋意放之。將三鐘同步,然後；搬上飛機；在搬的過程,兩座並列一起的鐘,必需同時搬運,始終保持同向同位子,另一鐘在飛機上與這兩鐘保持不同方向。飛機搬運過程,加速、減速、轉向,加速了時、頻效應,而並列一起的兩鐘,時、頻效應是保持同步進行的,所以同步了的兩鐘能保持較持久的同步,另一鐘與它們不同向,於是；時、頻效應對它與並列兩鐘的作用不同步,故；該鐘與並列兩鐘會很快失步！
在參照系S。內，有一電磁波發射源Ac與二個電磁波計數器A、B，Ac與A構成A鐘 。在S。系內還有一相對S。系靜止的慣性系S，在S系內還有一發射源Bc與B′電磁波計數器，構成B′鐘，Bc與B還構成B鐘。
三鐘；A鐘受Ac發射源電磁波控制，B與B′鐘受Bc發射源電磁波控制，它們都靜止於S。系內，Ac、Bc都是銫133原子輻射的電磁波發射源，三鐘都是接收了9192631770個周期電磁波數而跳秒，故，三鐘都是標準計時鐘，將三鐘同步。
當S系以0.5倍光速相對S。系運動，也就是Bc與B′ 以0.5倍光速向A、B運動，由時、頻效應知道，B鐘與A鐘、B′鐘失步了，B鐘變快了，A鐘是標準計時鐘，由結論(4)知道；B′鐘也是標準計時鐘。
B′鐘在跳秒的瞬間向A、B鐘發射了一個光脈衝訊號，B鐘在跳秒的瞬間接收到了光訊號，B′共發射了十個光脈衝訊號，十個光脈衝訊號前後時間間隔；B′鐘時間記錄為十秒，B鐘記錄時間也為十秒。而A鐘呢！記錄該事件的時間，由時、頻效應<1-4>式[t′=T。(1-CosαU。/C。)=10秒(1-0.5C。/C。)=5秒]知道為秒。
只要識別了光訊號的光譜，可用〈1－14〉式得知該事件的真時。如,紅移Z值為4的類星體(該類星體的視速率為光速的4倍),我們觀測該星體的事件時間為5秒,由<1-14>式進行轉換；該類星體所發生事件的真時間僅為1秒[T。=t。λ。/λ=t。λ。/(λ。+Δλ)=5秒/(1+4)=1秒] 。
結論(5)：要想得到被測天體的真時間，必須用<1-14>式進行時間轉換，即，必須把測者所在坐標系的觀測真時(地球時),轉換成被測事件坐標系的真時(天體時)。
Bc、B′越過A、B而正背離A、B以0.5倍光速運動，Bc、B′還是在十秒鐘內發射十個光訊號，A鐘的記錄由<1-4>式知道為十五秒。而B鐘由時、頻效應變慢了，但，時間記錄仍為十秒，由Bc傳送到B的媒介是電磁波，因時、頻效應使B鐘變慢(或快)了。光訊號由Bc、B′傳送到B的媒介也是電磁波，同樣會發生時、頻效應，使事件時間變長(或短)了，都是時、頻效應的結果，或者說；它們是相互彌補了，或相互抵消了，B鐘記錄事件的時間仍為S系內的真時，B為S系內發射源的電磁波所控制的時鐘，B為S系的本鐘，本鐘所記錄本系的事件時間，為本系事件的真時間。
結論(6)：本鐘只能記錄本系事件的時間，才為本系事件的真時間。地球上的計時鐘只能記錄地球上的事件時間才為真時間，地球上的鐘只是地球的本鐘,如記錄的是其他星球上事件的時間,必需由結論(5),進行轉換！
超光速天體
天空中響起隆隆轟鳴之聲，聽者抬頭望見一飛機；已飛越聽者上空，聽者吐口而說，“超音速飛機”；相信，人們都會認同，聽者言之無誤！這現象同樣適合超光速天體。
太空中一天體以超光速(4.5倍)運動，在未到達測者天頂附近前，測者是無法觀測到該天體，由<1-6>式知道,觀測光波波長不可為負值,只有當觀測波長大於零時,電磁波才被現代科技(文明)所觀察,因此存在一個臨界角α。[λ=λ。(1-CosαU。/C。)],也就是觀測波長λ為零時,超光速天體視分量角為臨界角, Cosα。U。/C。=1
Cosα。=C。/U。=C。/4,5C。Cosα。=1/4.5 α。=77.1604度 ,見圖<4> 圖中,測者在O點,超光速天體過了M。點的瞬間,才被測者觀測到,在M。之前,對於O點測者,接受的是負光波,至今從未報導過,那位科學家接收了負光波。圖中M至M。點,距離為D=1709.2587萬光年,天體以4.5倍光速運動,由M點運動到M。點,只需(t。=)379.8352萬年,光信息由M。點傳送到O點,時間為1025.6451萬年。該超光速天體由M點運動到M。點,再發射光信息傳送到O點,總共化時1405.4802萬年。而光信息由M點傳送到O點,需要2000萬年,兩者相差594.5198萬年。
這好象不可能的,但,在M點與M。點各存在一個光源,M點光源發射光信息後,也就是M。點光源滯後M點光源379.8352萬年後,再發射光信息,而O點測者接收到該光信息,要早於M點光源發射的光信息594.5198萬年。假如,無數個光源,由M點排至M。點,而且它們是在同一瞬間發射光信號,可以說,超光速天體由M點運動到M。點,是超距作用運動(超距作用是不存在的,但,超距作用現象,在宇宙空間是存在的!後面再探討),對於O點測者,最先接收到光信息的,是來至M。點,最晚接收的是來至M點,這無數個光源發射的是極短的光脈衝信號,對於O點的觀測者,卻發現的是單個光源；從M。點向M點自行,足自行了974.3549萬年(t-t′)。故我們還得到,在宇宙空間同時發生的事,在我們看來；是不同時的!而且還可以得到；對於O點測者；超光速天體速度越快,由臨界M。點倒自行至同一點(M)時間越長。
超光速天體在盲區是倒自行的,時間是倒流的,對一列超光速宇宙列車,在盲區是倒著開的,也就是,順序先後是倒著的。如果一星球,被測者觀察到的是；高度發達的文明社會的信息,在觀察過程；會逐漸向遠古原始時代退化,如同看電影,片子是倒著放,故事情節,是從末尾向開始倒敘。時間的確在倒流,即電磁波在”倒流”,電磁波為負值,地球文明還無法觀測到,如果超光速天體處在相對地球人的盲區(不同位置上的觀察者,有不同位段的盲區),而盲區此段宇宙空間,要是確是空無一物,那就成了名付其實的盲區!
宇宙高列正從宇宙隧道M。處通過,正被我們所拍攝到[這樣的機率,幾乎(拍攝)不存在],其照片就會呈顯兩列宇宙高列；一列為本影,朝運動方向自行,另一列為遺影,朝運動反方向倒自行^⑥(星系半人馬座A,此照片僅供閱覽,如果宇宙高列在宇宙隧道臨界點,都被我們所拍攝到,那天體超光速運動現象,在宇宙空間是普遍存在)!對於低速天體(低於光速),只存在紫移區與紅移區兩個區域,而這兩個區,都可以為無窮大區域。而宇宙高列(超光速天體),卻存在三個區域,紫移區、紅移區與盲區,紅移區與盲區可以為無窮大區域,但紫移區域並不是個無窮大區域,是個能被觀測到(可視)的有限小區域,如圖<4>中的4.5倍光速運動天體(通過測者最近距離ρ為1000萬光年),在紫移區能被測者(地球)所觀測的時間僅為25萬年。紫移區分別與紅移區、盲區之比,都分別趨於零!也就是,相對觀測者；超光速天體；在紫移區出現的機率是很小,天文觀察記錄中,會很少出現,有出現,未必識別。
2倍光速天體的臨界角為60度，從該臨界角自行至60度0分0.013秒，行程為0.84034366光年(ρ=1000萬光年)，2倍光速天體運行的時間為153.4704334天（0.42017183年），由時差方程知道[（t。+t1）-t=tx]，測者接收了2倍光速天體153.47天的光信息量，僅化了0.9467秒鐘（3x10^-8年）,可由<1-4>式來驗證,α角可取60度0分0.009秒,測者觀察時間為1秒,而該天體事件發生的真時間為153.146天,見圖<4-1>。由<1-6>式知道,由於時、頻效應,該天體在臨界處的可見光(α=60度0分0.01秒 U。=2C。 Z=2),都進入了[λ=λ。(1-CosαU。/C。)=(0.7∽0.4)微米X 1.09163854X10^-7]γ射線與高能宇宙射線^⑦,在紫移區超光速天體是可視天體,就是拍攝到光譜線,也難以識別紫移量。相對測者,2倍光速天體的視分量角(α)60.5度時,可見光只能進入紫外線區域。如果相對測者,天體在紫、紅移區域交界處(M′)附近,即是10倍光速運動的宇宙高列的紫、紅移量與一般(低於光速)天體的紫、紅移量,也無大的區別。
只有宇宙高列從宇宙隧道中通過,不管處於那個區域(盲、紫、紅)；都會激起宇宙介質的x、γ射線輻射及射電波輻射,只要隧道有足夠的長度,就會成為射線源,也就是；在塵埃較多的天區,較容易找到射線源,或；候選的源較多,源的射線強度隨介質的豐度而變化,在紫、紅移區域,有可視天體可對應。在臨界點附近,測者的觀察時間較為暫短,而且,自行值與倒自行值較大!見計算表<1>：我們將表中數據驗證一下；2倍光速,臨界角α=60度 t=L/C。=11547005.38年 第一年倒自行至β,β=α-θ(第一年)=59.97617959度, t2 =L2/C。=11549778.68年,t。′=(ρ/tgβ-ρ/tgα)/U。=2772.296年,將數據填入倒自行時差方程：tx=t2-(t。′+t)=1年(其他數據,讀者可以自行驗證)。由表中,我們還知道；α=π/2 時,天體年自行角值都小於0.04角秒(10倍光速,ρ=1000萬光年,α=π/2, Δ=0.2′),那,天體在紅移區其他區域；年自行值都會很小。
測者用一年的時間,得到2倍光速天體2772.296年的信息,或者說；觀測者在一年內看完了該天體；用2772.3年時間演的戲,而且觀測者是倒著看,從閉幕看到開幕!時間好象在倒流！
實質上,時間並不倒流,宇宙高列從宇宙隧道中通過,對於O點測者,該段隧道處於盲區,但,對於另一位置上的測者,該段隧道可能處於紫移區,或處於紅移區,那該測者觀察到該宇宙高列,是向前開的,並不倒自行,看到的,同樣的是這齣戲,是從啟幕開始看起,一直看到謝幕,時間並不倒流！
觀察到天體在倒自行,看到該天體的戲在倒演,就得出時間會倒流,顯然有誤。現做個假設實驗,在宇宙列車上,在列車中央,裝一頻率穩定的無線電波發射源,在列車首、尾各裝一無線電波計數器,構成共一發射源的二座子時鐘,二座子時鐘,可以同步,但,列車在加速過程,會很快失步,因,首計時鐘接收的電波路程在漸漸變大,時鐘在變慢,尾計時鐘接收的電波路程在漸漸變小,時鐘在變快。當列車速率到達光速,或超過光速,成了宇宙高列,高列首部的無線電波計數器,再也接收不到中部發射源的電磁波,時鐘仃止了,因光速有極限,宇宙高列的探照燈,朝前是不起作用的,是專朝後照的,車列尾部的無線電波計數器,還在繼續計數計時,如果宇宙高列是直線勻速超光速運動,那尾部時鐘計時,還是標準計時器，時鐘記錄的時間還為標準真時。不要因為首部時鐘仃止了,就得出時間也仃止了,這太誤導了！
宇宙天體不但是存在超光速運動,在運動過程還發生超距作用現象,宇宙高列從宇宙隧道中通過，隧道介質受激勵，發射射電波（包括x、γ射線）,發射的強度隨介質的豐度變化,觀測者的觀測靈敏度還與距離相關,在這裡我們只探討隧道截面。
截面是個園面,園面內的介質受天體契倫科夫輻射激勵的速度；由園心沿園面至邊緣（園環）受激的速度為光速,如果,測者至園心的視線；與園面垂直,那,園環各點至測者的距離相等,故,測者觀測到的環,是一正園環。園環是由園心點的光源；在同一瞬間被點亮的,園環各點,又在同一瞬間,向測者傳送光信息,經過相同路程,又在同一瞬間傳送到測者,故,測者看到的是一個；被同時點亮的正園環，也就是，測者視線至園心,與園面垂直時,測者看到的園環事件是同時的。
園環在同一瞬間被點亮,可以說；是宇宙空間的超距現象,如同一宇宙飛船，在一瞬間，繞了園環一周。如果，測者至園心的視線，與園面不垂直，與園面相交一個δ角,那，環的各點至測者的視程，不相等，環的各點在同一瞬間，向測者傳的送光信息，到達測者，是不同時，見圖<5>：園面與天體運動方向X軸垂直，O、M、P、P1各點在同一平面內(為測者X軸視向的視平面),園面與視平面相互垂直,交於PP1線段,P點為以R1為半徑的園環與PP1線段的交點,P點至O點測者,為該園環(R1為半徑)較其他各點的最近點,故,P點光信息最先到達測者,極次是M1點,最後是P1點。該環是同時被點亮的(超距作用現象),而測者觀察到的是；該環是從P點先亮,再從P點,沿環緣兩邊,漸向P1靠攏,漸漸點亮。
園面不只是一個環,是由無數個同心園環組成,測者觀察到的圖象,是由同一瞬間到達測者的光信息組成的,如同拍照,拍的是同一時間,進入像機底片的光信息。也就是,光信息由園心M點至P點（半徑為R1），再由P點至測者（光程為L1），所化光時為T,而光信息從園心至其他同心環各點,再至測者的所化光時也同為T, T=(R1+L1)/C。=(R2+L2)/C。=(R3+L3)/C。,所得圖像如圖<5>A中1環。因園面垂直於測者視平面,測者至M點的視線；在視平面內,故,線段MM2,垂直於OM線,測者經過t。時間間隔又拍攝了（A中）2環,M2點與M1受園心點激勵時間間隔為T。,t。為測者觀測時間,並不為觀測事件的真時(T。),因,測量角θ1與θ2都很小,由<1-4>式知道,α≈π/2,故,觀測時間t。約於觀測事件的真時T。(T。≈ t。),M1至M2點空間光程為 C。t。 。
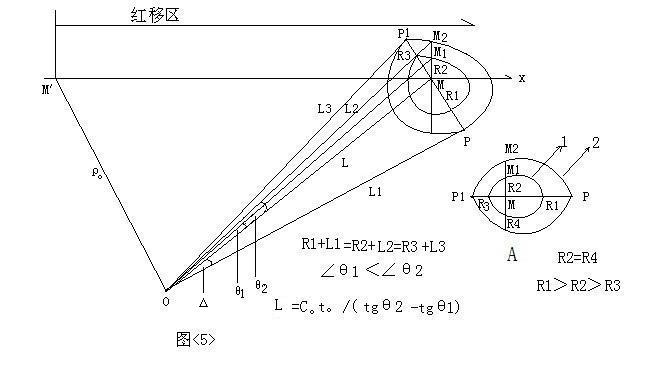
由1環與2環測得角∠M1OM為θ1 ,角∠M2OM為θ2 ,tgθ2ρ-tgθ1ρ=C。T。,整理得：
ρ=C。t。/(tgθ2-tgθ1) 。 <3-1>
退行的星系
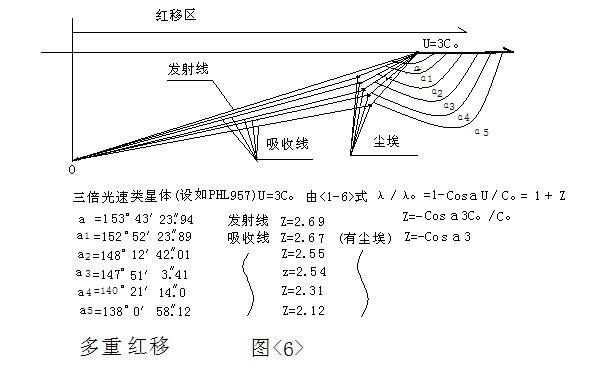
PHL 957為多重紅移類星體,其紅移值分別為；發射線Z = 2.69 、 吸收線分別為Z = 2.67、2,55、2.54、2.31、2.23 ,由哈勃定律【Vf=Hc×D Vf：遠離速率單位；Km/s 、Hc：哈勃常數單位；Km/（s·mpc） D：相對地球動距離單位；Mpc 百萬秒差距】^⑧，就會得出該天體與地球有六個不同的空間距離,顯然，這是不可能的，這是PHL 957類星體從宇宙隧道中經過,見圖<6>：發射線是PHL 957類星體的光線直射地球,也就是運動視速率分量角對著地球,而,吸收線的視速率分量角不是對著地球,該光線地球上的觀測者也不能直接接收到,是經過宇宙塵埃(塵埃受激),二次輻射,才被地球測者所接收。
宇宙空間是無邊無際的,天體向任一向運動；最終都要離地球而去,因,起初向著地球運動的天體,終將要越過地球,離地球而去！這是宇宙天體運動的規律,一切星系都要離銀河星系退行而去。作者認為：不可能存在；星系遇上宇宙壁,發生彈性碰撞,被退了回來，所以,星系都在退行,是必然的,是宇宙天體運動學的法則！
隨著時間推移,銀河星系會孤獨的在宇宙太空中遊蕩嗎？
遠古時代,先人觀看上天,到處都有無物的黑天區,自從望遠鏡發明之後,黑天區里卻是充滿星星與星雲,視野一下子大大的擴展了,不是宇宙空間在變大了,而是科學文明發展了。現在被觀察到的上100億光年的宇宙空間,還是一個很有限的空間,或,稱之為；銀河星系團(僅為宇宙的蒼海一粟),星系團以外的區域,現代地球科學文明還無法涉及,因,而現今的視野很有限,無法涉及銀河星系團之外。在銀河星系團之外,必然存在無數個河外星系[現代科學文明認為：星(系)體在宇宙空間；處處不斷的延生,又,不斷的消亡]。
從現代天體運動速率觀察來看,最有可能在我們視野中消失的；是超光速天體(類星體),一當離開了銀河星系團,就會在我們視野中消失,對於；大Z值的類星體,在觀察中,會最先逐漸暗淡,直至消失(在星體記載表上,原有記載的,而今觀察中,無緣無故的失蹤了,這,很可能是逃離了銀河星系團的逃失之星)。首選由河外星系團,而進入銀河星系團的星體,最有可能的；也會是高Z值的類星體。
我們巳探討過,超光速天體存在三個區域：
2倍光速； U。=2C。 α。= 60° (由Z= -C0sα。U。/C。式計箕) Z= -1 、
4,5倍光速： U。=4.5C。 α。=77°.16041159=77°09′37.48″ Z=-1 、
9倍光速： U。=9C。 α。=83°.62062979=83°14′14,27″ Z=-1 。
而且,超光速天體的速率越大,視速率分量臨角α。越大,對於相同的ρ。值,紫移區的區域越小,見圖<4>。
與測者最近距離(ρ。)為1000萬光年；
2倍光速運動的超光速天體,測者在紫移區可視的時間為133.9萬年,
4.5倍光速運動的超光速天體,測者在紫移區可視的時間為25萬年,
9倍光速運動的超光速天體,在紫移區可視的時間僅為6.1萬年,
由此知知；超光速天體速率越大,在紫移區可視的時間越短！故,在紫移區,超光速天體出現的幾率越少,另,即是被捕獲到,而現今,不一定被識別。
而入的超光速天體,首先要經歷盲區,在盲區；只有經過宇宙隧道(塵埃中通過)才被我們發現,而,只有超光速天體才會發生契倫科夫輻射,由<1-6>式知道；在臨界角位子上的塵埃,受到極高的契倫科夫能量輻射,因,在臨界角；天體所輻射的光譜能,都要進入了χ、γ譜能,甚至是宇宙射線能,故,受激的塵埃,會出χ、γ爆,甚至高能宇宙射線爆！當然,最基本的現象是射電源,其射電條文(年輪)如圖<5>A,不過,圖<5>在紅移區,而,在盲區,它的圖位,在X軸的相反方向的位子上,圖中PP′徑的長半徑MP指向相反方向。
可測距離
由圖<5>A知,射電條文圖；每一閉合條文為一變形橢園,它的長軸為R1+R3(R1>R3),短軸為
體可對應,在盲區(有塵埃的區域,超光速天體才有射電源),無可視天體可對應,如果該天體距離地
球較近,還許還有天體在塵埃中留有餘輝,被我們觀察到。
3C120射電源,作者的資料^⑨；距離為16億光年,觀測2年(1972年),它的直徑增大了0.001″
(如果是短軸的直徑),那么半徑(R)增大了0.0005″,也就是R+2光年=R2(C。t。=2光年),可有
<3-1>式計算：距離L=C。t。/(tgθ2 - tgθ1)=2光年/tg0°0′0.0005″=8.25億光年。
由<3-1>式知道；觀測半年,短軸半徑增大0.001″,C。t。=0.5光年,該射電源的距離(L)為
1.03億光年。
觀測一年：短軸半徑增大0.001″ L=2.06億光年(增大0.0001″L=20.6億光年)
觀測二年：短軸半徑增大0.001″ L=4.12億光年(增大0.0001″L=41,2億光年)
觀測三年：短軸半徑增大0.001″ L=6.18億光年(增大0.0001″L=61.8億光年)
觀測四年：短軸半徑增大0.001″ L=8.25億光年(增大0.0001″L=82.5億光年)
觀測五年：短軸半徑增大0.001″ L=10.3億光年(增大0.0001″L=103 億光年)
觀測十年：短軸半徑增大0.001″ L=20.6億光年(增大0.0001″L=206億光年？！)
由以上數據可知；觀測時間越長,短軸半徑增大值越小,所觀測的射電源距離的距離；也就越遠!
該射電源無可視天體對應,該是超光速天體,在盲區,見圖<7>。如；測的該射電源條文圖短軸半徑θ1為1.0″，過半年又測得θ2為1.001″，同時測得長軸半徑Δ為1.501″，可由圖<7>①式計算,
得距離L=103132403.1光年(1.03億光年),由②式求得短軸半徑R2=500.5光年,L2=103132403.1光年,由③式求得長軸長半徑R1=812.98光年,由④式求得超光速天體速率視分量角α=22.°60995169 = 22°36′35.83″,該射電源有可視天體對應,那么該射電源在紅移區,視速率分量角為α1=π-α′
,如無可視天體對應,那必在盲區,而且是倒自行,也就是長軸的長半徑指向天體運動(PP′與X軸在同一平面內)的反方向,該射電源；是超光速天體的遺影,那必還有本影；本影在M″處,可由⑤式求得
ρ值,由以數據(設超光速天體為5倍光速 U。=kC。=5C。)得ρ=72057602.15光年(0.72億光年) S2=(L-ρ)k, S2=155374004.8光年(1.55億光年)。
為什麼能同時測的本影與遺影,舉例：兩艘飛船同時從M點出發；一艘以光速飛向O點,另一艘以5倍光速沿X軸方向飛行,經過1.55億光年,到達M″處,改向,以光速飛向O點,經過0.72億光年,到達O點的瞬間；另一艘飛船從M點經過1.03億光年,也正到達O點(讀者可以計算,驗正)。
探討到此；給我們提出有意思的問題,測到本影,還可以測找到遺影。測到遺影,同樣可以測找到本影。
但,測下遺影射電條文圖,可以測知(L)距離,也可以測知視速率分量角(α),但在盲區,無可視天體對應時,也就無視紅移Z值,就無法求知超光速天體的真速率,也就無法求得X軸的M″點(本影點)。
如果測得是本影,同樣用圖<7>中；①、②、③、④、⑤式求得；距離L、視速率分量角α、由觀測所得視紅移值Z,可由Z=-CosαkC。/C。式(見圖<6>)求得光速倍數k值,由此測求知圖<7>中,紅移區M″處,所對應的盲區的射電遺影條文圖的位子M點。如果M處天區沒有塵埃呢？上面已探討過,超光速天體經過無介質(塵埃)的天區,就無射電輻射(介質二次輻射)發生。
正如觀察中,一千來個類星體,有射電源的只三百來個,這三百來個必有塵埃附著,那七百來個,必無塵埃！這么多的類星體與群多的射電源,必然存在本影與遺影同屬於一個超光速天體。
由表<2>知道；不管在那檔距離上,三年兩影分離速度,都是驚人的！
按常理；天體的年自行值,在天體的橫向(α=π/2)時,張角最大,其自行值也最大,由表<1>
知,不然,超光速天體的年自行最大值,卻在臨界點處,初三至五年自行值(與倒自行值)為最大,與常理相悖。
在其有塵埃的臨界點處,會出現γ、x爆,甚至宇宙射線爆,因,我們在第三節已探討過,由於時間效應,我們在一秒鐘時間內,接收了超光速天體其153.4天所激放的能量!所以,以"爆"的形式被我們所接收,而,塵埃天區出現的天體,其亮度會極烈徒增(光爆)!這一系列的“爆”,其原因；可稱得上,“時間效應”上的“時爆”！我們接收的是；超光速天體“時間”上的超級“壓縮彈”,壓縮比例為：13253760：1（153.4天為13253760秒）,壓縮倍數為1.3千萬倍,故,以“爆”的形式出現,也就不為怪了！
如果超光速天體,所在盲區,不是臨界點之處,那塵埃中,就無；可視天體,塵埃雲中,只遺留超光速天體的漫、反射的餘輝。第三節探討過,超光速天體的探照燈,朝前是不起作用,而是以扇形的形式朝向後方,由時、頻效應<1-5>式知道；臨界角(α。)位子處,契倫科夫輻射,施放的能量為最大,也就是扇桿位子方向為最大,正後方,扇中央為最小,故,塵埃雲隧道的兩側,餘輝(漫、反光)為最強,正後方為最弱,正前方,無餘輝,見圖<8>-②^⑩。在盲區,被我們首先發現之處；是塵埃雲隧道出口之處的射電文,因,在盲區,只存在遺影倒自行,故,首先被發現的,只能是隧道出口處盡頭的射電文,射電 文遺影只有從出口向進口倒自行。出口處的射電文,不會,一倒自行過後,射電文痕跡就消失,而是先滯留,經過好多年之後,才漸漸消退。這樣,倒自行之條文與滯留條文,會漸漸分離,而倒自行的條文圖,其長軸長半徑指向超光速天體運動的相反方向。
如果,半人馬座A事件,一開始發生,就被我們拍攝到,其射電文；是單一的射電指文圖,同時伴有γ、x射線,而今,半人馬座A實攝圖像,已分裂為；二個指文圖(見圖<8-1>)^⑾,與初時,單一的指文圖,在時間上,已相隔多年了,γ射線已漸漸消退,而留有X射線（見圖<8>-① ）。
實驗報告
雷達測速儀⑿,發射K波(頻率為ν。=24.150GHz),至移動物體(運動速度為U。),再反射回來,被雷達測速儀所接收,由時頻效應<1-12>式：
雷達測速儀在觀測過程，雷達波往返是瞬間完成，故，<1-12>式中；
β=α、V。=U。,由<1-12>式知道；當移動物體；正向著雷達測速儀或正背離雷達測速儀運動,也就是；視分量角α=0,或α=π時,測下移動物體的速度U=U。,但當分量角α≠0(或α≠π)時,測得移動物體速度U≠U。,被測移動物體的速率,只是視速率,將<1-12>式整理：
ν/ν。=(1+CosαU。/C。)(1+CosαU。/C。)/(1-CosαU。/C。)(1+CosαU。/C。)
(ν。+Δν)/ν。=(1+2CosαU。/C。+Cos^2α U。^2;。/C。^2;。)/(1-Cos^2α U。^2/C。^2)
1+Δν/ν。=(2CosαU。/C。)/(1-Cos^2α U。^2;。/C。^2;。)+(1+Cos^2α U。^2。/C^2)/(1-Cos^2α U。^2/C。^2)
因；C。遠大於U。,故,U。^2/C。^2 趨於0,得上式為：
1+Δν/ν。=2CosαU。/C。+1 整理得：
Δν=2U。ν。Cosα/C。 <6-1> U。=ΔνC。/2Cosαν。 <6-2>
當汽車（U。=30m/S,時速為108Km/h）在公路上,勻速直線行駛時,相對公路傍靜止觀測的雷達測速儀,一路上,由遠處向著雷達測速儀行駛,行至雷達測速儀傍,再漸漸遠離雷達測速儀而去,相對雷達測速儀的視分量角α隋行駛距離變化而變化,由<6-1>式知道,視分量角α的變化,測下的頻差Δν也在變化的,見表<3>。現行市場所出購的雷達測速儀與交警所用的雷達測速儀，計算內件，都沒有對視分量角α進行修正，不是根據<6-2>式進行計算，而是略去式中的Cosα,而成U。=ΔνC。/2ν。式,現行雷達測速儀的速度計算內件,根據上式對所測頻差Δν,進行計算,作者在2012年2月15日（18日、19日）,上午約09時至09時30分,在溫州甌海大道,天晴、微風、氣溫3～8°C,用風火輪J2360雷達測速儀﹙測速範圍：0.4-321Km/h,帶列印記錄﹚實地自駕車來回幾天的觀測,選取相應的有用記錄數據, 見表<3>實測速度項；現行雷達測速儀觀測的只是視速率(U),並不是移動物體的運動真速率(U。),要想得到其真速率,必須對現行雷達測速儀,進行改正,加一指向針(見圖<9>),指向針方向與物體移動方向,兩方向線平行,指針指向移動物體運動反方向,雷達測速儀微波射槍與指向針的夾角,與移動物體的視分量角,互為內、外錯角,微波射槍自動跟蹤移動物體,其視分量角α成了已知角,由圖<9>知,所接收的頻差Δν由<6-2>式：U。=ΔνC。/2Cosαν。的測速儀內件進行計算,得出移動物體的真速率,見表<3>真速雷達計算速度項。現行的雷達測速儀,作者所做的測定,與第二節結論③時,所論述的一樣；紫移效應時,所觀測的移動物體運動速度越來越慢,紅移效應時,測得移動物體的速度越來越快,交警隋時隋地都可以做該實驗,都可以為之見證!
解題
夫妻同齡,30歲生一子。兒子出生時,丈夫乘坐速率為0.86C。的飛船去半人馬座α星,並且立即返回。已知半人馬座α星與地球距離為4.3 l.y.(光年),並設飛船相對地球一去一回作勻速直線運動。當丈夫返回地球時,妻子、兒子和丈夫各為多大年齡？丈夫往返時間為10年(4.3 l.y.÷0.86C。×2),按相對論得出兩個結果：
②按相對論,飛船也可以設為參照靜止系,地球相對飛船運動,地球的時鐘變慢了,其結果；妻子35歲,兒子5歲,丈夫40歲。
事實上,這是"雙子佯謬"的翻版,自從相對論問世以來就一直爭論至今,並產生各種歧義。
但，存在相對運動的坐標系之間，存在時間相對性，會發生時間效應，飛船以0,86C。的速率由地球飛往半人馬座α星,歷時5年經過4.3 l.y.路程,到達半人馬座α星,飛船時鐘記錄下飛船從地球飛往半人馬座α星的時間為5年。
由<1-4>式 t′=T。(1-CosαU。/C。)知道,∵ T。=5年、α=π、U。=0.86C。∴ t′=9.3年 ,飛船時鐘記錄下飛船從地球到半人馬座α星曆時5年,而地球時鐘記錄卻為9.3年,地球時鐘記錄錯了嗎？沒有,可以驗證；
飛船飛離地球的瞬間,飛船發射光訊號f1,到達α星的瞬間飛船發射光訊號f2,兩訊號之間的時間間隔,飛船時鐘記錄為5年,因,飛船由地球飛往半人馬座α星,歷時5年,f2光訊號是在半人馬座α星上發射的,α星與地球相距4.3光年,f2光訊號還要經歷4.3年才能到達地球,故,地球時鐘記錄寸下；f1與f2光訊號的時間間隔為9.3年,f2與f1光訊號不是在同一地點發射的,它們的光程不相等（光程相差4.3光年）,由結論⑵知道,當兩光訊號以不同的光程到達接收者時會發生時間效應。
由<1-6>式知,λ/λ。=1-CosαU。/C。, ∵α=π
∴λ/λ。=1+U。/C。=1+0.86, λ/λ。=(λ。+Δλ)/λ。
=1+Δλ/λ。=1+Z=1+0.86 (Z=0.86)
由結論⑸知,要想得到被測天體事件的真時間,必須用<1-14>式進行時間轉換,即,必須把測者所在坐標系的觀測真時(地球時),轉換成被測事件坐標系的真時(天體時),<1-14>式 T。=t′λ。/λ=9.3年/(1+0.86),T．=5年 。
地球觀測者測得飛船從地球飛往半人馬座α星,觀測時間為9.3年,但,由結論⑸得到該事件的真時為5年。
飛船去是5年,自然返也是5年,但,觀測結果又是如何,將；T。=5年、α=0、U。=0.86C。代入<1-4>式t″=T。(1-CosαU。/C。),∵ α=0 U。=0.86C。 ∴ t″=0.7年。
驗證：光訊號f2在半人馬座α星發射,經過4.3光年,到達地球,而被地球觀測者所接收的瞬間開始計時（光訊號f2是經歷時4.3年被地球測者所接收）,而飛船此瞬間已不在半人馬座α星了，已飛離半人馬座α星3.698光年(0.86C。×4.3年)的距離,此瞬間飛船離地球只有0.602光年（4.3光年-3.698光年）了,此時飛船再到達地球只需0.7年(0.602光年÷0.86C。)了,到達地球的瞬間發射光訊號f3, 光訊號f2與光訊號f3 的真時間間隔為5年,地球觀測者的觀測時間卻只是0.7年。
如果把觀測時間t′（9.3年地球時）作為被測事件的真時,其結果會得出錯誤的結果；飛船由地球飛至半人馬座α星的時間為9.3年,由此得出半人馬座α星離地球的距離為7.998光年(0.86C。×9.3年),或飛船飛行速率為0.46C。(4.3光年÷9.3年)。
飛船由半人馬座α星返回地球的觀測時間為0.7年,其結果會得出半人馬座α星離地球的距離只有0.602光年(0.86C。×0.7年),或認為飛船返回地球的速率為6.14C。(4.3光年÷0.7年)。
很顯然會得出錯誤的結論與結果。
