時間尺度

時間尺度（Time scale）完成某一種物理過程所花費時間的平均度量。一般來講，物理過程的演變越慢，其時間尺度越長，物理過程涉及的空間範圍越大，其時間尺度也越長。

基本介紹

• 中文名：時間尺度
• 外文名：Time scale
• 定義：物理過程所花費時間的平均度量
• 學科：物理學
• 性質：多面性
• 代表人物：普朗克

定義

時間尺度（Time scale）完成某一種物理過程所花費時間的平均度量。一般來講，物理過程的演變越慢，其時間尺度越長，物理過程涉及的空間範圍越大，其時間尺度也越長。

內容

時間標準

時間標準是一種測量時間的規範：要么是時間通過的速度，要么是時間點，要么是兩者都有。在現代，一些時間規範已經被正式認定為標準，以前它們是習慣和實踐的問題。一個時間尺度的例子可以是指定一個度量時間劃分的方法。一個民用時間的標準可以指定時間間隔。

標準化時間測量是利用時鐘來計算一些周期性變化的周期，這可能是自然現象的變化，也可能是人工機器的變化。

歷史上，時間標準通常是基於地球的自轉周期。從17世紀晚期到19世紀，人們認為地球的日轉動速度是恆定的。在19世紀，對包括日蝕或月蝕記錄在內的幾種不同類型的天文觀測，引起了人們的懷疑，即地球自轉的速度正在逐漸放緩，也顯示出小規模的不規則現象，這在20世紀早期得到證實。根據地球的軌道周期和月球運動的實際情況，從1952年開始的天文觀測中，以地球自轉為基礎的時間標準被取代(或最初補充)。在1955年，銫原子鐘的發明導致了更古老和純粹的天文時間標準的更替，這是出於大多數實際的目的，在新的時間標準的基礎上完全或部分的原子時間。

各種類型的二和日被用作大多數時間尺度的基本時間間隔。其他時間間隔(分鐘、時間和年份)通常是根據這兩個定義的。

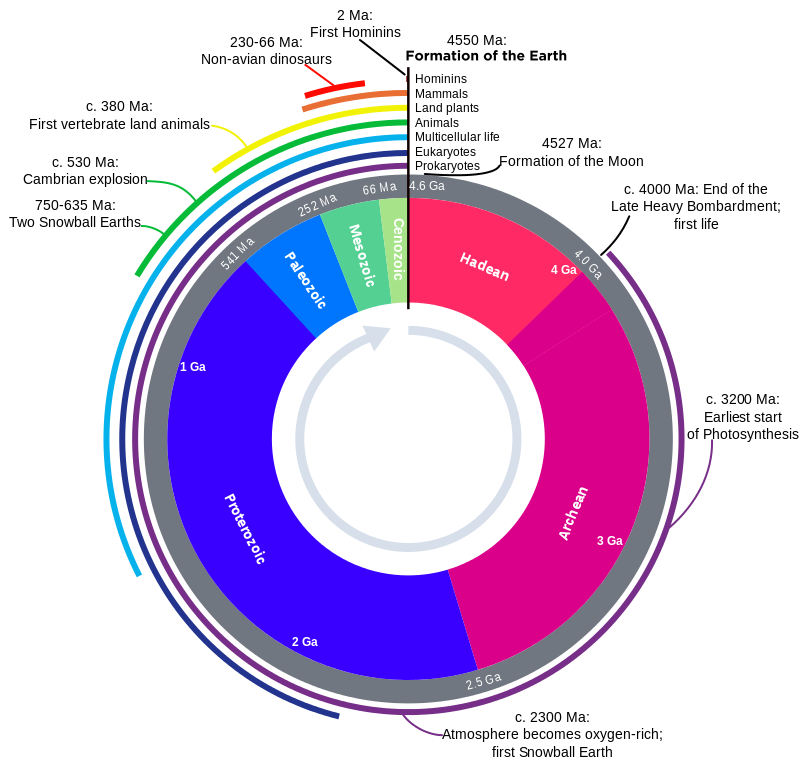
地質學的時間尺度

地質年代尺度(GTS)是一個按時間順序排列的系統，它將地質地層(地層學)與時間聯繫起來，並被地質學家、古生物學家和其他地球科學家用來描述地球歷史上發生的事件的時間和關係。在這裡展示的地質時期的表，與國際地層學委員會規定的命名法、日期和標準顏色一致。

來自放射測定年代的證據表明地球大約有45億年的歷史。根據每段時期發生的事件，將地球過去的地質或深層時間組織成不同的單位。在GTS上的不同時間跨度通常是由與它們相對應的地層組成的變化所標記，並指出主要的地質或古生物事件，如大規模滅絕。例如，白堊紀和古第三紀的界限是由白堊紀-古基因滅絕事件定義的，這標誌著非鳥類恐龍和許多其他生命群體的滅亡。更早的時間跨度，早於可靠的化石記錄(在元古代之前)，是由它們的絕對年齡定義的。

太陽系內的其他一些行星和衛星有足夠堅硬的結構，保存著自己的歷史記錄，例如金星、火星和地球的衛星。像氣態巨行星這樣具有支配地位的流體行星，並沒有以可比的方式保存它們的歷史。除了晚期的猛烈撞擊之外，其他行星上的事件可能對地球沒有直接的影響，地球上的事件對這些行星的影響也相對較小。因此，建造連線行星的時間尺度，只與地球的時間尺度有關，除非是在太陽系的背景下。後期重轟炸的存在、時間和地面效應仍在爭論中。

核能的時間尺度

在天體物理學中，核時間尺度是一個恆星的生命周期的估計，僅僅基於它的燃料消耗速率。除了熱和動力時間尺度之外，它還被用來估計某一顆恆星在其生命的某一階段和它的生命周期中所存在的時間長度。在現實中,恆星的壽命大於所估計的核時間尺度,因為作為一個燃料變得稀缺,另一個通常將其替代氫燃燒了氦燃燒,等。然而,所有的氫燃燒後階段結合通常加起來不到10%的氫燃燒的持續時間。

熱時間尺度

在天體物理學中，熱時間尺度或克爾維-亥姆霍茲時間尺度是一顆恆星以其當前光度速率輻射出其總動能含量的近似時間。隨著核和動力學的時間尺度，它被用來估計某一顆恆星在其生命的某一階段和它的壽命，如果滿足假設條件的話。在現實中，恆星的壽命比熱時尺度估計的要大，因為一種燃料變得稀缺，另一種將取代它的位置——氫燃燒讓位給燃燒的氦，取而代之的是碳燃燒。

普朗克時間尺度

經典廣義相對論的奇性不可避免，所以標準大爆炸模型中時空存在著零點，給了上帝一個容身之地。但是考慮到量子力學的測不準原理，一些基本量度，譬如長度和時間具有測不準性。測不準的程度由普朗克常數確定，從該常數可以定出最小的長度量子，即普朗克長度，為10E-33厘米，這遠遠小於原子核的尺度。測量任何長度不可能比這個更精確，而且比普朗克長度更短的長度是沒有意義的。同樣，作為時間量子的最小間隔，即普朗克時間，為10E-43秒。沒有比這更短的時間存在。這就是說，我們不可能把黑洞縮減為數學上的一個點，同樣也不能追溯到大爆炸的真正開始時刻。

普朗克長度l=gh/c3~10-35m=10E-33厘米(約等於)

普朗克常數記為 h ，是一個物理常數，用以描述量子大小。在量子力學中占有重要的角色，馬克斯·普朗克在1900年研究物體熱輻射的規律時發現，只有假定電磁波的發射和吸收不是連續的，而是一份一份地進行的，計算的結果才能和試驗結果是相符。這樣的一份能量叫做能量子，每一份能量子等於hv，v為輻射電磁波的頻率，h為一常量，叫為普朗克常數。普朗克常數的值約為:

h=4.13566743(35)×10^（-15） eV·s

其中電子伏特(eV)·秒(s)為能量單位:

普朗克常數的物理單位為能量乘上時間，也可視為動量乘上位移量:

(牛頓(N)·米(m)·秒(s))為角動量單位

另一個常用的量為約化普朗克常數(reduced Planck constant)，有時稱為狄拉克常數(Dirac constant)，紀念保羅·狄拉克:

其中 π 為圓周率常數 pi。 念為 "h-bar" 。

普朗克常數用以描述量子化，微觀下的粒子，例如電子及光子，在一確定的物理性質下具有一連續範圍內的可能數值。例如，一束具有固定頻率 ν 的光，其能量 E 可為:

有時使用角頻率 ω=2πν :

許多物理量可以量子化。譬如角動量量子化。 J 為一個具有旋轉不變數的系統全部的角動量， Jz 為沿某特定方向上所測得的角動量。其值:

因此， 可稱為 "角動量量子"。

普朗克常數也使用於海森堡不確定原理。在位移測量上的不確定量(標準差) Δx ，和同方向在動量測量上的不確定量 Δp，有如下關係:

還有其他組物理測量量依循這樣的關係，例如能量和時間。

時間尺度微積分

在數學中，時間尺度微積分是差分方程理論與微分方程理論的統一，統一積分微分學與有限差分的微積分，為研究混合離散連續動力系統提供了一種形式主義。它在任何需要同時建模離散和連續數據的領域都有套用。它給出了一個導數的新定義如果一個函式微分一個函式它作用於實數那么這個定義就等價於標準微分，但是如果一個函式作用於整數，那么它就等於正向差分運算元。