在動力氣象學研究中,不同類型的大氣運動各自由特定的大氣控制方程進行表述。尺度分析指,根據某種運動中各物理量實際尺度的大小(特徵值),來估計其運動方程中對應各項的大小,從而保留貢獻較大項,略去貢獻較小項,使方程得到簡化的一種方法。
基本介紹
- 中文名:尺度分析
- 外文名:scale analysis
- 相關術語:大氣運動
- 學科分支:動力氣象學
意義,尺度分類,簡化過程,
意義
但是,由天氣的實踐經驗可以知道,影響大氣運動的各個物理因子,如慣性力、重力、氣壓梯度力等,在實際不同規模的運動系統中,貢獻的大小是不一樣的,差距有可能很懸殊,因此,針對不同類型的運動特徵和規律,必須突出方程中對應該類型起決定作用的主要因子,忽略次要因子,也就是說,要針對研究對象進行方程的簡化。簡化後的方程,不僅便於計算,而且利於揭示某種運動形式的本質特徵,便於實際套用。
尺度分類
尺度分析時,通常先按系統的水平、垂直和時間特徵尺度將運動系統分類。
然後確定方程中各項物理因子的尺度:
(1) 各場變數的數量級;
(2) 各場變數的變化幅度;
(3) 出現這些變化的特徵長度、厚度和時間尺度。
在確定尺度時,為了使數值保持在合適範圍內,通常用10的整數次冪表示數量級。
簡化過程
將同一級別系統的特徵尺度帶入方程,並僅保留同量級項,就可以得到適合不同條件大氣運動的簡化方程。
以垂直運動的預報方程舉例:

經過尺度分析,式中第2項氣壓梯度力與第3項重力為同一數量級,其餘兩項相比之下要小4個數量級,可以忽略不計。於是,原方程可簡化為下式:
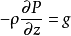
即原垂直運動預報方程由一個簡化了的,關於氣壓的診斷方程代替了。
