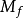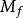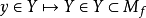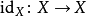映射柱

在數學的代數拓撲分支中，拓撲空間X 與Y 之間函式f 的映射柱（mapping cylinder）是將任何一個映射用一個在如下意義下等價的上纖維化代替的方法。

基本介紹

• 中文名：映射柱
• 外文名：mapping cylinder
• 學科：代數拓撲
• 領域：代數拓撲

定義

在數學的代數拓撲分支中，拓撲空間X與Y之間函式f 的映射柱（mapping cylinder）是將任何一個映射用一個在如下意義下等價的上纖維化代替的方法：

給定映射 ，映射柱由一個空間 與一個上纖維化 以及滿同倫等價（事實上，Y是 的形變收縮）組成，使得複合等於f。

這樣空間Y被一個同倫等價的空間 取代，映射f被提升映射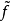 代替。等價地，

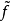
圖表

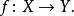
被圖表

與這兩個圖表之間的一個同倫等價取代。

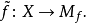
這個構造用於將拓撲空間之間的映射用拓撲等價的上纖維化取代。注意逐點一個上纖維化是一個閉包含映射。

構造

M_f的正式定義如下：

這裡l是單位區間， 表示兩個拓撲空間的不交並， 是把 等同起來的等價關係（將柱 的一個底面通過f與Y黏合起來）。從而非正式地說，映射柱 是把 的一個底面用f黏貼到Y得到的構造。

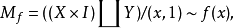
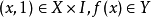
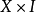
定義 為 （將X包含到另一個底面）。定義 為 而在M_f的Y部分為恆同。根據等價關係~這是良定義的。

注意到Y是 的形變收縮。

投影 分裂（通過 ），形變收縮（取時間參數為s）由下式給出：

（這裡所有Y中的點不動，從而是一個形變收縮。）

套用

映射柱將關於子空間或空間包含的定理運用到到不必是單射的一般映射。

因此，那些與空間、所涉及映射的同倫類無關的定理或方法（比如同調、上同調或同倫理論本身）可能可適用到X,Y,f，這裡假設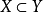 以及 f事實上是子空間的包含。另外，這個構造更本質的吸引之處是它與通常心理的印象一個函式是將 X中的點“送到” Y中的點一致，從而X 嵌入Y 中也是（儘管函式不必是一對一的）。這個構造給出了一個圖像同倫等價於直覺的那個，這表明直覺圖像是正確的只要Y的形變不是一個阻礙。

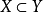
範疇套用與解釋

我們可以用映射柱構造同倫極限：給定一個圖表，將其中的映射用上纖維化代替（利用映射柱），然後取通常的逐點極限（需多些注意，但映射柱是其中一部分）。

相反地，映射柱是圖表的同倫推出，這裡 而 。

映射望遠鏡

給定映射序列

映射望遠鏡是同倫正向極限。如果所有這些映射已經是上纖維化（比如正交群），則正向極限是並集，但是一般情形必須使用映射望遠鏡。映射望遠鏡是一個映射柱序列，底面和底面相連。這個構造的圖像看起來像堆起來的變大的柱子，即像一個望遠鏡，從而有這樣的名稱。

映射望遠鏡的正式定義為

另見

• 映射柱 (同調代數)
  
• 非豪斯多夫映射柱