基本介紹
- 中文名:星形線
- 外文名:astroid
- 周長:6*a
- 面積:(3*π*a^2)/8
- 旋轉體表面積: (12*π* a^2)/5
- 旋轉體體積:(32*π*a^3)/105
- 套用學科:幾何學
- 又名:四尖瓣線
簡介,詳細介紹,星形線的性質,星形線的套用,
簡介
星形線(Astroid)星形線的方程 星形線
星形線
 星形線
星形線直角坐標方程:x2/3+y2/3=a2/3
參數方程:x=a*(cost)3,y=a*(sint)3 (t為參數)
它所包圍的面積為3πa2/8。
它與x軸圍成的區域繞x軸旋轉而成的旋轉體表面積為12πa2/5。
體積為32πa3/105。
詳細介紹

若讓一個半徑為1/4的圓在一個半徑為1的圓內部,延著圓的圓周旋轉,小圓圓周上的任一點形成的軌跡即為星形線。星形線的參數方程為:


因此星形線為六次曲線,在實數平面上有四個尖瓣的奇點,分別是星形線的四個頂點,在無限遠處還有二個複數的尖瓣的奇點,四個重根的複數奇點,因此星形線共有十個奇點。
一個半徑為 a之圓的內擺線構成的星形線,其面積為 ,周長為6a。
,周長為6a。

星形線的性質
最先對星形線進行研究是Johann Bernouli。星形線由於有四個尖端,所以有時也被稱為四尖內擺線(tetracuspid)。星形線於1836年被正式定名,首次出現在正式出版的圖書(出版於維也納)中。星形線還有許多有趣的名稱:cubocycloid和paracycle。 圖片來自維基百科詞條:星形線
圖片來自維基百科詞條:星形線
 圖片來自維基百科詞條:星形線
圖片來自維基百科詞條:星形線T: x*sin(p)+y*cos(p)=a*sin(2p)/2 。
如果切線T分別交x、y軸於點x(X,0)、y(0,Y),則線段xy恆為常數,且為a。
星形線是由半徑為a/4的圓在半徑為a的內側轉動形成的。
(陰影里的另一個弧是圓的一部分以做對比)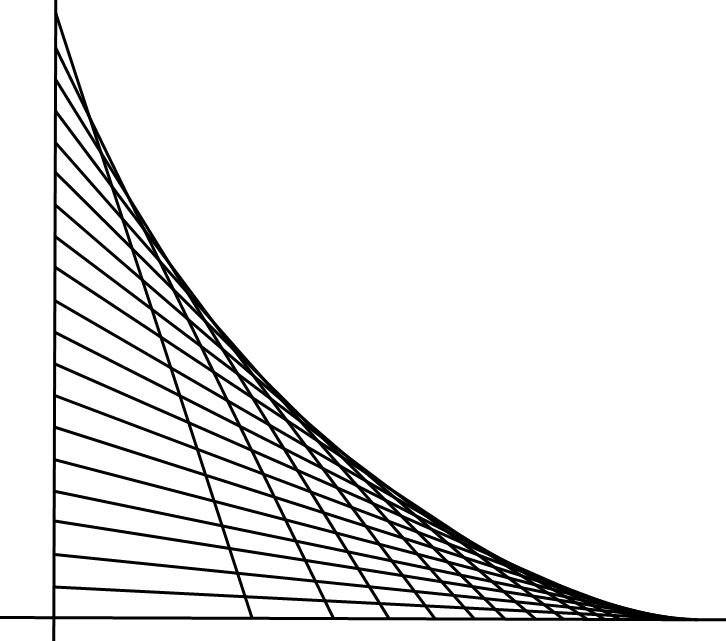 定長線段滑動的包絡線:星形線
定長線段滑動的包絡線:星形線
 定長線段滑動的包絡線:星形線
定長線段滑動的包絡線:星形線 圓弧與星形線
圓弧與星形線星形線的套用
星形線與汽車門
我們知道,世界上有許多偉大的建築,門的設計也是建築家特別注意的。但是,最普通的門只有兩種:完整一扇和對開的兩扇。普通的房門是完整的一扇,一般的校門是對開的兩扇,而公共汽車的門不但是對開的兩扇,而且每一扇都由相同的兩半用鉸鏈鉸接而成。開門關門時,以靠近門軸的半扇繞著門軸旋轉,另半扇的外端沿著連線兩個門軸的滑槽滑動,開門時一扇門折攏成為半扇,關門時又重新伸展成一扇。公共汽車的這個特殊門是根據星形線設計製造的。



