斯梅爾馬蹄(Smale's horseshoe)由美國數學家史蒂芬·斯梅爾(Stephen Smale)提出的一種形狀類似於馬蹄的離散動力系統。
基本介紹
- 中文名:斯梅爾馬蹄
- 外文名:Smale's horseshoe
- 適用領域:數學,動力
- 提出者:史蒂芬·斯梅爾
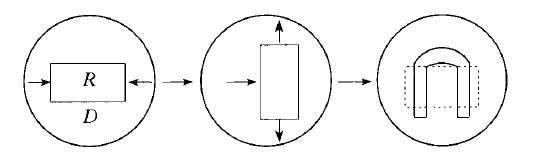
斯梅爾馬蹄(Smale's horseshoe)由美國數學家史蒂芬·斯梅爾(Stephen Smale)提出的一種形狀類似於馬蹄的離散動力系統。

斯梅爾馬蹄(Smale's horseshoe)由美國數學家史蒂芬·斯梅爾(Stephen Smale)提出的一種形狀類似於馬蹄的離散動力系統。簡介斯梅爾馬蹄(Smale's horseshoe)由斯梅爾(Smale ,...
史蒂芬·斯梅爾 美國數學家,1930年7月15日生於美國密執安州福林特。18歲考入密執安大學,1952年畢業,1966年獲得菲爾茲獎,2007年獲得沃爾夫獎。他因證出五維或以上的龐加萊猜想而成名。然後轉向研究動力系統,作出重要成就,還勾劃出...
斯梅爾是1966年菲爾茲數學大獎得主,他是一位有著獨特人生經歷的當代數學大師。他在數學的許多領域中做出了卓越成就,例如首先證明將球體從內向外翻轉在理論上是可能的,提出了混沌概念的先聲——斯梅爾馬蹄等等。斯梅爾首先突破了維數障礙,...
恩龍映射是一個數學術語。恩龍映射(Henon map)斯梅爾馬蹄的一個具體的例子.設F是二維平面內的方塊Q:-R=x=R, -R毛y毛R上的映射,若(x,y)=F(x,y),F'的解析表示式如下:所以F'是雙方單一連續可微的.在映射F之下,直線x=k...
(3)套用“一個平面映射存在斯梅爾馬蹄變換,該映射就是具有反映渾沌屬性的不變集”的原理,採用梅爾尼科夫方法來判定系統具有斯樂馬蹄變換意義下的渾沌,從而得到該系統發生渾沌現象的判據。論文中分別給出四邊簡支矩形板和固定邊圓形板的...
穩定性猜測(stability conjecture),是指關於穩定性的兩個猜測,它是微分動力系統理論研究的核心內容。起源 斯梅爾(Smale , S.)總結了莫爾斯一斯梅爾系統、安諾索夫系統、斯梅爾馬蹄等有關結構穩定性的若干結論後,在1967年,提出以下兩個...
《混沌的微擾判據》是1994年上海科技教育出版社出版的圖書,作者是劉曾榮。作品目錄 目 錄 非線性科學叢書出版說明 前 言 第1章 預備知識 1符號動力系統 2斯梅爾馬蹄變換 3橫截同宿點理論 第2章 梅爾尼科夫方法 4平面哈密頓系統 5 ...
相比之下,公理 A 微分同胚由於只有有限個鏈傳遞分支,動力形態就相對簡單(即使各個鏈傳遞分支內部可能有斯梅爾馬蹄那樣的複雜程度)。如果把馬蹄這樣的不變集看成是一個複雜化了的“鞍點”,把雙曲吸引子和排斥子看成是一個複雜化了...
12.5 非自治擾動的梅利尼科夫方法232 第13章 高維系統中的混沌235 13.1 斯梅爾馬蹄235 13.2 斯梅爾-伯克霍夫同宿定理236 13.3 同宿軌道的梅利尼科夫方法237 參考文獻241 記號術語表243 索引244 ...
10.1 斯梅爾馬蹄 10.2 轉移不變集 10.3 拓撲熵映射的連續性 第4章 有限型子轉移與非負方陣 11 非負方陣 11.1 不可約性和非周期性 11.2 非負方陣的有向圖 12 有限型子轉移的轉移方陣 12.1 轉移方陣 12.2 轉移方陣的...
以佩克索托對二維流形結構穩定系統的特徵研究為藍本,斯梅爾將其推廣到一般流形上,稱之為莫爾斯-斯梅爾系統,並證明其為結構穩定的。但隨後舉出不屬於這種系統的結構穩定系統,例如,托姆環面雙曲自同構和安諾索夫微分同胚以及斯梅爾馬蹄,它們...
2.3.3 斯梅爾馬蹄映射 2.4 埃儂吸引子 2.4.1 二維映射 2.4.2 埃儂映射 2.4.3 埃儂吸引子 2.5 標準映射 2.5.1 標準映射的不動點 2.5.2 標準映射相圖 思考題與練習題 參考文獻 第3章 連續系統動力學 3.1 非線性...
實際上斯梅爾的馬蹄映射也會形成康托爾集。康托三分集 取一條長度為1的直線段,將它三等分,去掉中間一段,留剩下兩段,再將剩下的兩段再分別三等分,各去掉中間一段,剩下更短的四段,……,將這樣的操作一直繼續下去,直至無窮...
但是最常見的構造是康托爾三分點集,由去掉一條線段的中間三分之一得出。康托爾自己只附帶介紹了三分點集的構造,作為一個更加一般的想法——一個無處稠密的完備集的例子。實際上斯梅爾的馬蹄映射也會形成康托爾集。
