斯坦納－雷姆斯定理

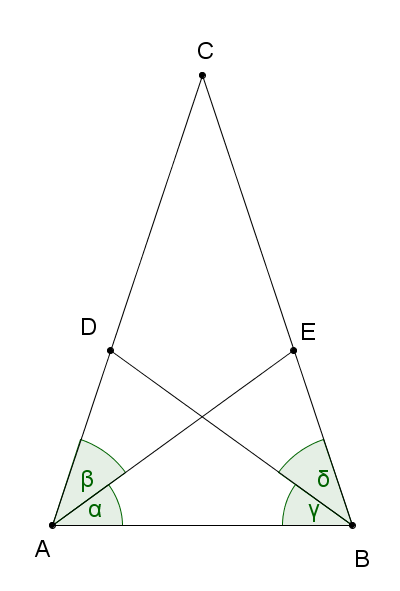
斯坦納-雷姆斯定理說明：有三角形ABC，D、E點分別在AC、BC上，使得BD、AE分別為角ABC及角BAC的內角平分線。若BD=AE，則BC=AC。

基本介紹

• 中文名：斯坦納－雷姆斯定理
• 外文名：Steiner–Lehmus theorem
• 分類：數理科學

定義

類似的陳述適用於中線、高、內角n分線（將原來的角分成原來的1/n角的線段）和經過葛爾剛點的線[1]等的塞瓦線段。可是這並不適用於外角平分線。一個132度、36度和12度的三角形是一個反例。

這個定理是魯道夫·雷姆斯（Ludolph Lehmus）向雅可比·斯坦納提出的。

表述

這一命題的逆命題“等腰三角形兩底角的平分線長相等”早在二千多年前歐幾里得的《幾何原本》中就已作為定理，證明是很容易的。但上述原命題在《幾何原本》中卻是隻字未提，一直直到1840年，雷姆斯（C.L.Lehmus）在他給斯圖姆（C.Sturm）的信中提出請求給出一個純幾何證明。但斯圖姆未能解決，就向許多數學家提出這一問題。首先給出證明的是瑞士幾何學家斯坦納（J.Steiner,1796—1863），因而這一定理就稱為斯坦納-雷姆斯定理。

後世發展

斯坦納的證明發表後，引起了數學界極大反響。論證這個定理的文章發表在1842年到1864年的幾乎每一年的各種雜誌上。後來，一家數學刊物公開徵解，竟然收集並整理了60多種證法，編成一本書。直到1980年，美國《數學老師》月刊還登載了這個定理的研究現狀，隨後又收到了2000多封來信，增補了20多種證法並收到了一個最簡單的直接證法。經過幾代人的努力，100多年的研究，“斯坦納-雷姆斯”定理已成為數學百花園中最惹人喜愛的瑰麗花朵。