基本介紹
- 中文名:熱爾崗點
- 外文名:Gergonne point
- 所屬學科:數學
- 所屬問題:平面幾何(三角形)
- 簡介:三角形三條特殊直線的交點
- 相關概念:納格爾點
基本介紹,熱爾崗點的證明,相關結論,
基本介紹
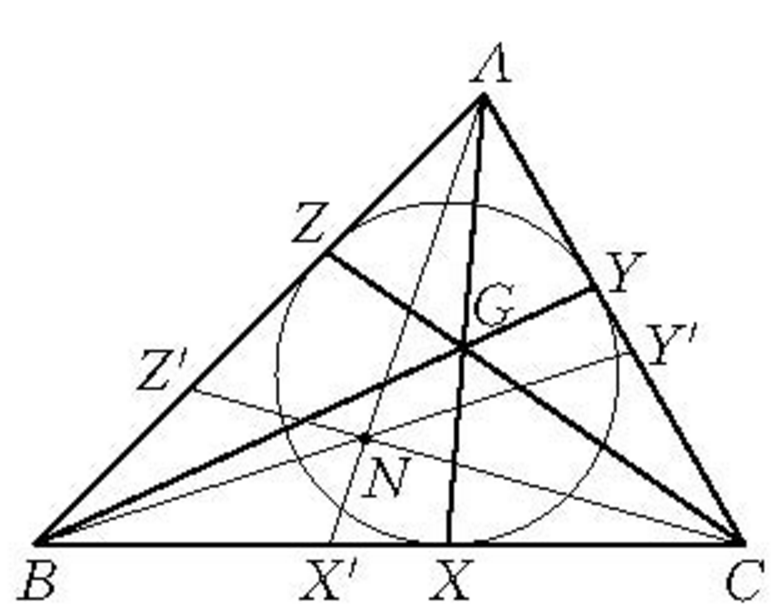
熱爾崗定理 分別連線三角形一個頂點及對邊上的內切圓切點的三條直線共點。
這個點被稱為此三角形的熱爾崗點。
熱爾崗點的證明
證明 在圖1中,圓O與AB、AC、BC三邊分別相切於N、M、L三點。
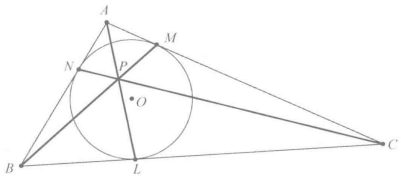 圖1
圖1由此可得AN=AM,BL=BN,CM=CL。這些等式可以寫成
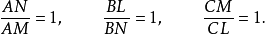
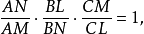
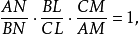
相關結論
⑴ 三角形的內切圓切於BC,CA,AB三邊於D,E,F三點,則AD,BE,CF交於一點,該點稱為熱爾崗(Gergonne)點,以Ge記之。
類似地,三角形三個旁切圓在BC,CA,AB三邊上的切點,分別是D',E' ,F' ,則AD',BE' ,CF'交於一點,該點稱為奈格爾(Nagel)點,以Na記之。
⑵ 現在把內切圓與旁切圓統一聯繫起來,設在BC邊上兩個圓的切點分別是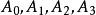 ;在AC邊上兩個圓的切點分別是
;在AC邊上兩個圓的切點分別是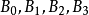 ;在AB邊上兩個圓的切點分別是
;在AB邊上兩個圓的切點分別是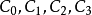 ,則有
,則有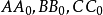 交會於Ge,
交會於Ge,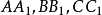 交會於G1,
交會於G1,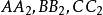 交會於G2,
交會於G2,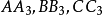 交會於G3,這是四個熱爾崗點。
交會於G3,這是四個熱爾崗點。
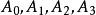
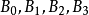
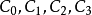
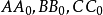
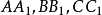
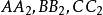
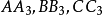
又有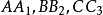 交會於Na,
交會於Na,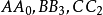 交會於N1,
交會於N1,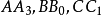 交會於N2,
交會於N2,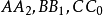 交會於N3,這是四個奈格爾點。
交會於N3,這是四個奈格爾點。
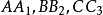
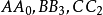
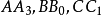
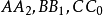
證明 如圖(a),設D,E,F關於AI,BI,CI的對稱點為A',B',C',則不難知AA',BB',CC'為AD,BE,CF的等角線,所以AD,BE,CF交於P(熱爾崗點)的等角共軛點為P'(AA',BB',CC交點)。
因為A'B1=DC1,C'B2=EA1,DC1=EA1,所以A'B1=C'B2,故A'C'//AC,同理C'B'//CB,B'A'//BA,所以三角形A'B'C'與△ABC關於P'位似,故⊙I與⊙ABC也關於P'位似,即⊙I與⊙ABC相似中心為P'。
如圖(b),設ID,IE,IF交⊙I於另一點D1,E1,F1,則不難導出AD1,BE1,CF1為AD,BE,CF的等截線,所以AD1,BE1,CF1交於一點R(納格爾點)。
設D2,E2,F2是D1,E1,F1關於IA,IB,IC的對稱點,有AD2,BE2,CF2為AD1,BE1,CF1的等角線,因此它們必交於一點R'(R的等角共軛點)。
如圖(b),設ID,IE,IF交⊙I於另一點D1,E1,F1,則不難導出AD1,BE1,CF1為AD,BE,CF的等截線,所以AD1,BE1,CF1交於一點R(納格爾點)。
設D2,E2,F2是D1,E1,F1關於IA,IB,IC的對稱點,有AD2,BE2,CF2為AD1,BE1,CF1的等角線,因此它們必交於一點R'(R的等角共軛點)。
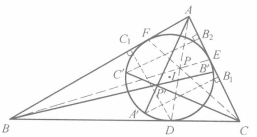 圖2(a)
圖2(a)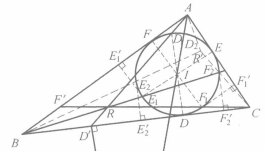 圖2(b)
圖2(b)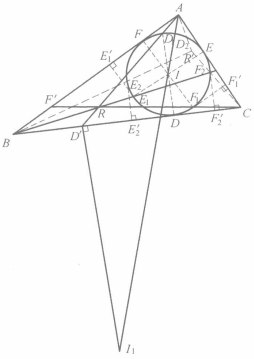 圖 2(b)
圖 2(b)⑷ 熱爾崗點有一個有趣的推廣。
定理△ABC的內切圓切BC,CA,AB於D,E,F三點,另作一與內切圓的同心圓⊙R,ID,IE,IF的延長線交⊙R於D',E',F',則AD',BE',CF'三線共點 (圖3)。
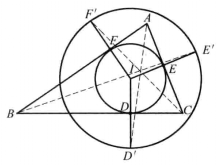 圖3
圖3⑸ 原三角形中的熱爾崗點也是下列三角形中的幾何特徵點:內切點三角形中的共軛重心;反補三角形中的M點;內心垂足三角形中的共軛重心;垂心的反垂足三角形中的M點;內切點三角形中的餘弦圓圓心等等。
第一三角形 | 第二三角形 |
△ABC | 中點三角形的外切點三角形 |
△ABC | 內切點三角形的等角中線三角形 |
內切點三角形 | 熱爾崗點的反切瓦三角形 |
內切點三角形 | 熱爾崗點的外接切瓦三角形 |
△ABC | 垂心的隅角三角形中的內切圓和外接圓的內相似中心三角形 |
△ABC | 內切圓和外接圓的內相似中心對旁心三角形各邊的反射點三角形 |
△ABC | 熱爾崗點對內切點三角形各頂點的反射三角形 |
△ABC | 熱爾崗點對熱爾崗點的反切瓦三角形各頂點的反射三角形 |
△ABC | 形心的隅角三角形中的熱爾崗點三角形(位似) |