基本介紹
- 中文名:改進離散餘弦變換
- 外文名:Modified Discrete Cosine Transform
- 簡稱:MDCT
- 提出者:Princen J和Bradley A
- 提出時間:1986年
- 快速算法:基於FFT算法、基於DCT算法
概念介紹
定義




特性



快速算法

直接算法

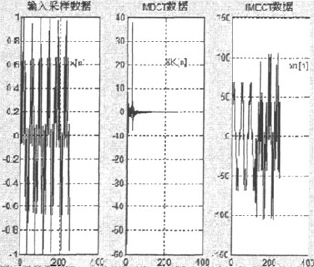
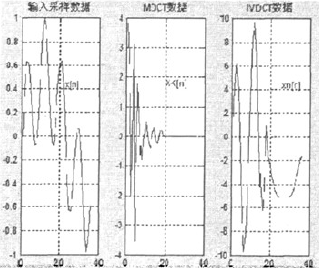
基於FFT算法












基於DCT算法

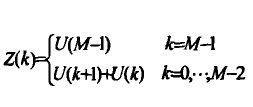
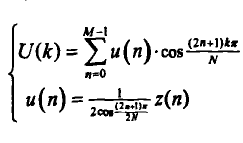
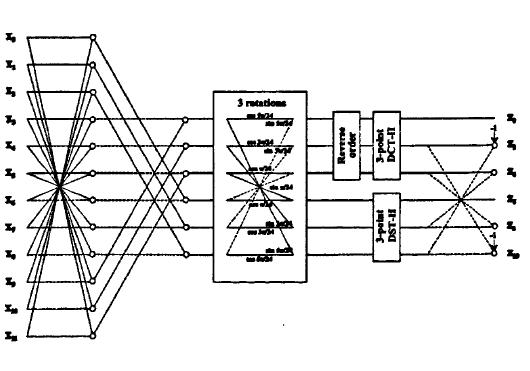
























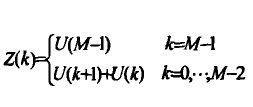
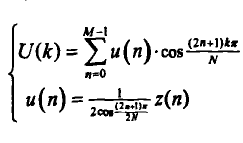
改進離散餘弦變換(Modified Discrete Cosine Transform ),簡稱MDCT,是一種線性正交交疊變換。它使用了一種時域混疊抵消技術(TDAC),包含50%的時域交疊窗,在不降低編碼性能的情況下...
改進離散餘弦變換 改進離散餘弦變換(Modified Discrete Cosine Transform ),簡稱MDCT,是一種線性正交交疊變換。它使用了一種時域混疊抵消技術(TDAC),包含50%的時域交疊窗,在不降低編碼性能的情況下有效地克服加窗離散餘弦變換(DCT)塊...
《一類離散正交變換的快速算法及套用研究》是依託東南大學,由舒華忠擔任項目負責人的面上項目。中文摘要 離散正交變換是數位訊號和圖像處理等領域重要的工具,本項目著重考慮改進的離散餘弦變換(MDCT)、複數調製重疊變換(MCLT)、離散Hartley...
變換編碼是於1968年Pratt首先提出,採用傅立葉變換。後來相繼出現了Walsh變換、斜變換、k-l變換以及離散餘弦變換(DCT)等。變換編碼 變換編碼不是直接對空域圖像信號進行編碼,而是首先將空域圖像信號映射變換到另一個正交矢量空間(變換域...
完成基於一階矩的傅立葉變換、餘弦變換,正弦變換、改進的離散餘弦變換、小波變換、W變換、卷積、自相關和互相關快速算法以及構築以上算法的脈動式陣列,進行了以上各種算法的硬體實現研究。我們在基於一階矩的卷積器和相關器上取得了重大...
8?13共軛梯度快速傅立葉變換(CG-FFT)226 8?14改進型離散餘弦變換(MDCT)226 8?15奇疊加TDAC235 8?16感知變換音頻編碼器237 8?17OCF編碼器238 8?18NMR評估系統239 8?19移動接收音頻編碼器240 8?20高質量音樂信號的自適應功率...
還有,這裡我們所要說的變換(transform)雖然是數學意義上的變換,但跟函式變換是不同的,函式變換是符合一一映射準則的,對於離散數位訊號處理(DSP),有許多的變換:傅立葉變換、拉普拉斯變換、Z變換、希爾伯特變換、離散餘弦變換等,這些...
這個模組採用了改進離散餘弦變換MDCT,它是一種線性正交交迭變換,使用了一種稱為時域混迭取消TDAC(timedomainaliasingcancellation)技術。MDCT使用KBD(Kaiser-Besselderived)視窗或者使用正弦(sine)視窗,正向MDCT變換可使用下式表示:逆向MDCT...
3.2.1 離散餘弦變換(DCT) 86 3.2.2 改進的離散餘弦變換(MDCT) 87 3.2.3 基於提升格式的整數MDCT實現 89 3.2.4 無損壓縮實現流程 90 3.2.5 仿真結果 94 任務3.3 圖像/視頻信息的霍夫曼編碼 95 3.3.1 圖像/視頻...
建立擾動力的關係模型,確定擾動狀態的辨識參數,實現擾動狀態的量化與分級;然後研究擾動力與視覺圖像模糊程度的關係,進行模糊圖像分類;進一步探索基於圖像分類的模糊圖像處理方法,通過改進圖像復原算法中的離散餘弦變換法,有效求取圖像模糊...
破壞性音訊壓縮通常涉及使用時域/頻域變換,例如改進的離散餘弦變換。基於心理聲學模型,我們可以利用遮蔽效應,像是頻域遮蔽及時域遮蔽,使得不會記錄到不會被注意到的聲音。例如,在一般情況下,人類不能察覺到一個與音量較大的聲音同時...
5.7.1 Chirp-z變換原理 (123)5.7.2 Chirp-z變換的FFT實現 (124)*5.8 離散餘弦變換及其FFT實現 (125)5.8.1 離散餘弦變換 (125)5.8.2 離散餘弦變換的FFT實現 (125)*5.9 FFT套用於線性相關的快速...
第3章 圖像變換 3.1 傅立葉變換 3.1.1 一維傅立葉變換 3.1.2 二維傅立葉變換 3.1.3 二維離散傅立葉變換的性質 3.1.4 正交變換的基本概念 3.2 離散餘弦變換 3.2.1 離散餘弦變換的定義 3.2.2 離散餘弦變換的快速...
頻域去模糊方法,圖像在頻域上進行處理,即對相應的係數進行變換,再將處理後的圖像進行逆變換。將圖像從空間域轉換到頻域方法很多,如傅立葉變換、小波變換和離散餘弦變換等。而傅立葉變換和小波變換則是常見的用於圖像去噪的變換方法。...
全書共分三部分,基礎理論部分主要介紹並行計算平台、並行算法概論、並行程式開發環境等;基礎套用部分包含矩陣運算、快速傅立葉變換、卷積運算、數字濾波、離散餘弦變換、哈達瑪變換、2D離散小波變換、數字圖像處理等方面的並行算法設計、分析...
第5章 圖像時頻變換 5.1 Fourier變換 5.1.1 Fourier變換的性質 5.1.2 離散Fourier變換 5.1.3 二維離散Fourier變換的性質 5.2 快速傅立葉變換 5.2.1 計算DFT的問題及其改進途徑 5.2.2 FFT算法及其原理 5.3 離散餘弦變換 ...
