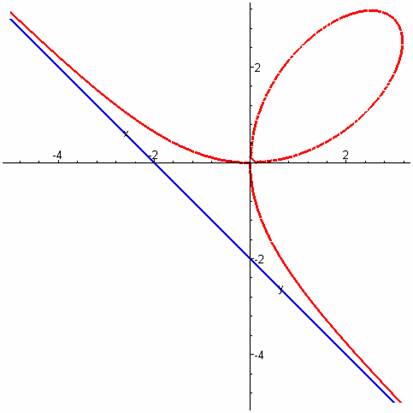
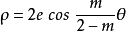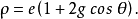擺線族曲線亦稱旋輪類曲線 ,是各種旋輪線的統稱,廣泛套用於圖案設計、齒輪設計和機油泵、旋轉活塞發動機的缸體輪廓線等方面。
基本介紹
- 中文名:擺線族曲線
- 外文名:cycloid family curve
- 適用範圍:數理科學
簡介,套用,
簡介
擺線族曲線亦稱旋輪類曲線 (cycloidal curve),是各種旋輪線的統稱。
長短幅圓內、外旋輪線的方程可以統一寫成
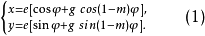
式中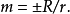 當 m>1 時是長(短)幅圓內旋輪線;當 m<1 時是長(短)幅圓外旋輪線。g=l/e 稱為形狀係數。
當 m>1 時是長(短)幅圓內旋輪線;當 m<1 時是長(短)幅圓外旋輪線。g=l/e 稱為形狀係數。 表示母圓與基圓中心間的距離,稱為偏心距。基圓 O 的半徑
表示母圓與基圓中心間的距離,稱為偏心距。基圓 O 的半徑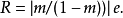 曲線上點 M(φ) 處的法線必過母圓 Q 的轉動瞬心
曲線上點 M(φ) 處的法線必過母圓 Q 的轉動瞬心
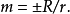

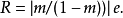
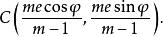


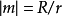
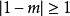
1、若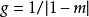 (即l=r),則曲線(1)為圓內(外)旋輪線(有尖點)。
(即l=r),則曲線(1)為圓內(外)旋輪線(有尖點)。
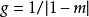
2、若 (即l>r),則曲線為長幅圓內(外)旋輪線。
(即l>r),則曲線為長幅圓內(外)旋輪線。

3、若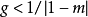 (即l<r),則曲線為短幅圓內(外)旋輪線。
(即l<r),則曲線為短幅圓內(外)旋輪線。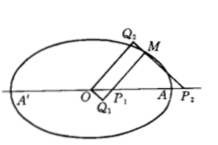 圖1.
圖1.
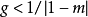
 圖1.
圖1.套用
旋輪類曲線是由兩個勻速旋轉運動合成的:點 Q 繞定點 O 旋轉的時候,同時動點 M 繞點 Q 旋轉,兩個旋轉的角速度之比為 1-m。每一條旋輪類曲線可以有兩種不同的創立方法,兩曲線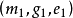 與
與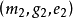 若且唯若
若且唯若
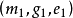
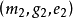
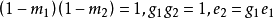

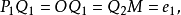
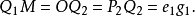
當形狀係數 g=1 時,圖形是玫瑰線