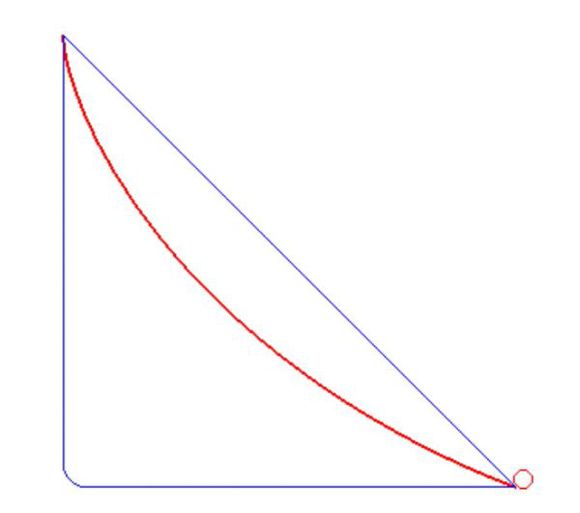
兩點之間一小球滾下,不是直線的連線下降最快,而是小球在最速曲線上滾下最快。
基本介紹
- 中文名:最速曲線
- 外文名:brachistochrone curve
簡介,其他性質,
簡介
在一個斜面上,擺兩條軌道,一條是直線,一條是曲線,起點高度以及終點高度都相同。兩個質量、大小一樣的小球同時從起點向下滑落,曲線的小球反而先到終點。這是由於曲線軌道上的小球先達到最高速度,所以先到達。然而,兩點之間的直線只有一條,曲線卻有無數條,那么,哪一條才是最快的呢?伽利略於1630年提出了這個問題,當時他認為這條線應該是一條直線,可是後來人們發現這個答案是錯誤的。1696年,瑞士數學家約翰·伯努利解決了這個問題,他還拿這個問題向其他數學家提出了公開挑戰。牛頓、萊布尼茲、洛比達以及雅克布·伯努利等解決了這個問題。這條最速曲線就是一條擺線,也叫旋輪線。
旋輪線
義大利科學家伽利略在1630年提出一個分析學的基本問題——“一個質點在重力作用下,從一個給定點到不在它垂直下方的另一點,如果不計摩擦力,問沿著什麼曲線滑下所需時間最短。”。他說這曲線是圓,可是這是一個錯誤的答案。
瑞士數學家約翰.伯努利在1696年再提出這個最速曲線的問題(problem of brachistochrone),徵求解答。次年已有多位數學家得到正確答案,其中包括牛頓、萊布尼茲、洛必達和伯努利家族的成員。這問題的正確答案是連線兩個點上凹的唯一一段旋輪線。
旋輪線與1673年荷蘭科學家惠更斯討論的擺線相同。因為鐘錶擺錘作一次完全擺動所用的時間相等,所以擺線(旋輪線)又稱等時曲線。
看一個稍微有點振奮人心的東西,Johann Bernoulli 對最速曲線問題的beautiful解答:
如果使分成的層數n無限地增加,即每層的厚度無限地變薄,則質點的運動便趨於空間A、B兩點間質點運動的真實情況,此時折線也就無限增多,其形狀就趨近我們所要求的曲線——最速曲線.而折線的每一段趨向於曲線的切線,因而得出最速曲線的一個重要性質:任意一點上切線和鉛垂線所成的角度的餘弦與該點落下的高度的平方根的比是常數.而具有這種性質的曲線就是擺線.所謂擺線,它是一個圓沿著一條直線滾動(無滑動)時,圓周上任意一點的軌跡。
因此,最速曲線就是擺線,只不過在最速曲線問題中,這條擺線是上、下顛倒過來的罷了.
經過論證和科學實驗,圖中紅色路線是最快的路線,即“最速曲線”。最速曲線的形狀為曲線,起始近乎垂直加速,讓物體獲得了快速通過後半程水平位移的能力,平均速度最快。

其他性質
初始坐標不同的物體在相同最速曲線上向下滑運動,同一時刻抵達終點。