基本介紹
- 中文名：旋輪類曲線
- 外文名：cycloidal curve
- 別稱：擺線族曲線
- 領域：數學
- 釋義：各種旋輪線的統稱
- 分類：外切外擺線、漸開線等
分類,外切外擺線,漸開線,內切外擺線,內擺線,直滾擺線,擺線族曲線的基本性質,
分類
旋輪類曲線可分為：外切外擺線、漸開線、內切外擺線、內擺線和直滾擺線。該分類的規律是：
（1）從外切外擺線到漸開線是滾圓曲率半徑由小變無限大；
（2）從漸開線到內切外擺線是滾圓曲率改變方向
（3）從內切外擺線到內擺線是滾圓曲率半徑由大變到小於基圓半徑；
（4）從內擺線到直滾擺線是基圓曲率半徑由小變無限大。
從這個變化規律可以看出擺線和漸開線是性質上相同的曲線，可以把它們歸入一族，將它們取名為擺線族曲線。
外切外擺線
外切外擺線是指：滾圓與基圓外切並沿基圓作純滾動時，滾圓上定點的軌跡是外切外擺線。如圖1所示。
圖1 外切外擺線漸開線
若滾圓曲率半徑加大到無限大，圓周展成一條直線，該直線與基圓相切並沿基圓作純滾動，直線上定點的軌跡為漸開線。如圖2所示。
圖2 漸近線內切外擺線
若上述沿基圓滾動的直線向下彎曲，變成一個比基圓半徑更大的滾圓，該滾圓與基圓內切並沿基圓作純滾動，滾圓上定點的軌跡是內切外擺線。如圖3所示。
圖3 內切外擺線內擺線
若內切外擺線滾圓的曲率半徑縮小到小於基圓半徑，該滾圓與基圓內切並沿基圓作純滾動，滾圓上定點的軌跡為內擺線。如圖4所示。
圖4 內擺線直滾擺線
若內擺線的基圓半徑加大到無限大，基圓圓周展成一條直線，滾圓與該直線相切並沿直線作純滾動，滾圓上定點的軌跡為直滾擺線。如圖5所示。
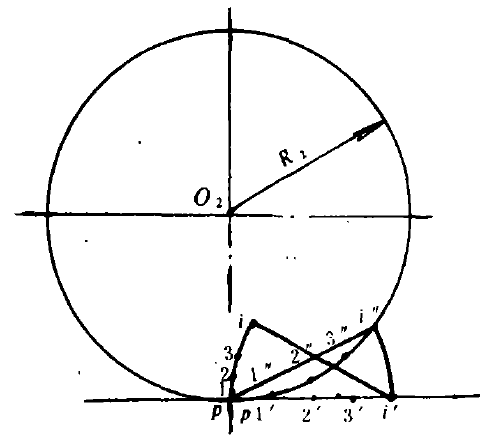圖5 直滾擺線擺線族曲線的基本性質
擺線族曲線有以下兩種性質：
(1) 廣義的滾圓(弧線或直線)與廣義的基圓(弧線或直線)相切，它們在滾動過程中走過的行程相等(如圖1所示)。根據這一性質就有：
(2) 廣義滾圓(弧線或直線)上任意兩點作正向和反向滾動所形成的軌跡具有完全的對稱性(如圖1所示)。根據這一性質就有：
