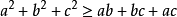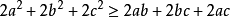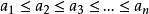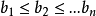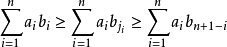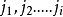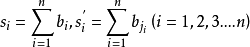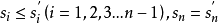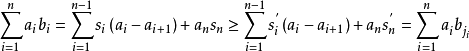排序不等式是數學上的一種不等式。它可以推導出很多有名的不等式，例如：算術幾何平均不等式(簡稱算幾不等式)、柯西不等式、切比雪夫總和不等式。排序不等式（sequence inequality,又稱排序原理）是高中數學競賽大綱、新課標 普通高中課程標準試驗教科書（人民教育出版社）數學（選修4-5 第三講第三節） 要求的基本不等式。
基本介紹
- 中文名：排序不等式
- 外文名：Rearrangement inequality
- 別稱：排序原理
- 學科：數學
說明,套用,排序不等式的證明,
說明
排序不等式表述如下，設有兩組數a1,a2,……an和b1,b2,……bn，滿足a1≤a2≤……≤an,b1≤b2≤……≤bn，c1,c2,……cn是b1,b2,……bn的亂序排列，則有a1bn+a2bn-1+……+anb1≤a1c1+a2c2+……+ancn≤a1b1+a2b2+anbn,若且唯若a1=a2=……=an或b1=b2=……=bn時等號成立。一般為了便於記憶，常記為：反序和≤亂序和≤順序和.
套用
設a,b,c≥0
,則ab+bc+ca的最大值為_______.
【解題指南】由於a,b,c的地位是均等的，不妨設a≥b≥c≥0，然後利用排序不等式求解.
【解析】由排序不等式
，得ab+bc+ca≤3.即ab+bc+ca的最大值為3.
答案：3
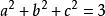
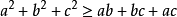
排序不等式的證明
①分析法
要證
只需證
只需證
根據基本不等式
∴原結論正確
②設有兩個有序數組：
及
求證：
(順序和≥亂序和≥逆序和)
其中
是自然數的任何一個排列
證明：令
由題設易知 
因為
故
所以 
即左端不等式，類似可證明右端不等式
