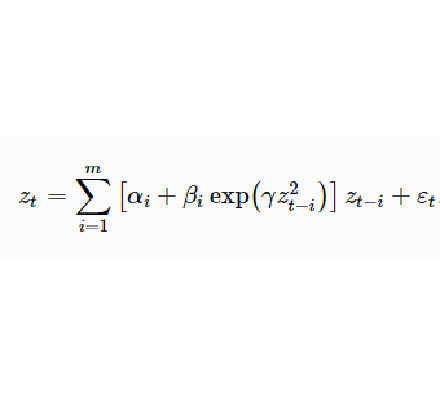指數自回歸模型

指數自回歸模型(exponential autoregressive models)是一種非線性模型，它是尾崎(T.Ozaki)和哈根(V.Haggan)在1978年為研究非線性隨機振動理論而提出的。非線性時間序列包含了非線性系統中各種變數的過去信息，同時蘊含著大量關於系統演變的規律和趨勢。這樣的時間序列往往是不可逆的、非線性相依的、偏態的，並且存在著廣泛的頻幅相依特性。為此，20 世紀80 年代初尾崎(Ozaki)和哈根(Haggan)提出了指數自回歸模型(exponential auto-regressive model，EXAR 模型)，它可以復現非線性隨機振動的某些特性，反映時間序列的頻幅相依性。用加拿大山貓數據建立EXAR模型，結果表明、擬合的殘差方差比門限自回歸模型和AR(2)模型都小，且求得的山貓時間系列周期與實際情況相吻合。指數自回歸模型在工程中已有一些套用。

基本介紹

• 中文名：指數自回歸模型
• 外文名：exponential autoregressive models
• 所屬學科：數學（統計學）
• 簡寫：EXAR 模型
• 所屬問題：時間序列分析

結構及特點

EXAR模型源於二階非線性隨機振動微分方程

式中， 表示對時間 的二階導數 元表示對時間t的一階導數；“阻尼力” 和“恢復力" 是非線性函式； 為獨立白噪聲。當 是線性函式時，則式(1)為二階線性微分方程。當 為白噪聲時，輸出 含有的周期隨振幅變化,即所謂的“頻幅相依”。尾崎根據上述效應提出了二階指數自回歸模型：

式中 分別依賴於 這種依賴關係為指數函式形式：

推而廣之，m階EXAR模型的結構為：

式中 和 為模型參數。

特點

EXAR模型的特點：

①能刻畫非線性特性。模型參數 是隨時間變化的,其值取決於 同時又刻畫了 與 之間呈指數形式的非線性關係。

②能產生突躍現象。從 中可看出，當 很大時 趨近於 而當 很小時 近似等於 其間變化關係是連續的。當 從最大值到最小值時就產生突躍現象。

參數估計

在非線性時間序列分析中，參數辨識的方法主要有最小二乘法、極大似然法等。哈根基於最小二乘法給出了EXAR模型的參數辨識方法：

(1) 先固定值，按最小二乘法作對的歸分析，估計和。用AIC確定模型階數m。

(2) 在一定範圍內取不同值，重複第(1)步的做法，得到不同值對應的參數和AIC值。

(3) 選擇AIC最小對應的模型參數即為所求。

上述參數辨識方法是可行的，但計算量大，且不一定能找到最優點，因而不是一種較好的方法。為此，提出了參數辨識的AGA，它包括如下兩個步驟：

第一步： 用自相關分析技術確定EXAR模型的自回歸項。時間序列延遲k步的自相關係數的方差隨k的增大而增大，的估計精度隨k的增加而降低，因此k應取較小的數值。

根據的抽樣分布理論，在置信水平的情況下，推斷與之間的相依性是否顯著。EXAR模型的自回歸項應與這些相依性顯著的項相對應，其中相依性顯著的最大延遲步數即為模型的階數m。

第二步：用AGA直接在相對殘差平方和最小化下同時最佳化模型各參數，即求如下最小化問題：

式中，為擬合值。