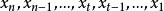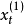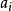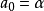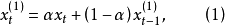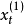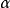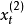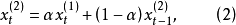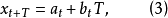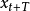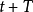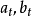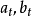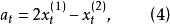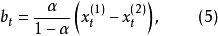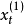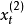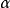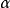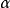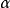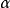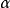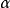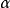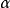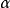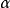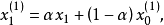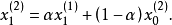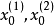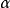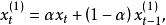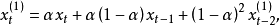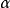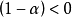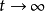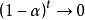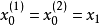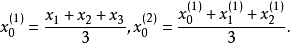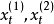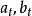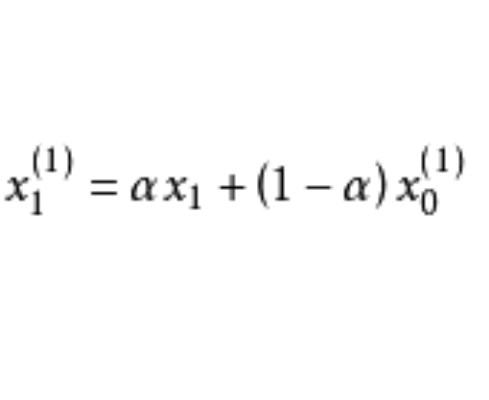指數滑動平均法簡稱為指數平滑法。是利用上一期的實際值和預測值(估算值)，對它們進行不同的加權分配，求得一個指數平滑值，作為下一期預測值的一種預測方法。它的預測公式是：Xt=αSt-1+(1-α)Xt-1，(0<α<1)，式中，Xt為第t期預測值，St-1為上一期實際值；Xt-1為上一期預測值；α為加權係數。指數平滑法是在移動平均法基礎上發展起來的，它具有移動平均法的優點，又可以減少運算過程中的數據儲存量，同時還考慮了不同時期的數據所起的不同作用。採用指數平滑法的關鍵是確定α值。一般情況下，α值的大小，既和反映近期數據的能力有關，也和數據波動狀況有關。通常不直接利用一次指數平滑法來預測，而是利用二次指數平滑法，求出平滑係數，建立起預測模型，再進行預測。三次以上指數平滑法幾乎適用於所有的時間序列預測，但在套用上有不少問題，所以實際上使用不多。
基本介紹
- 中文名：指數滑動平均法
- 外文名：exponential moving average method
- 所屬學科：數理統計
- 別稱：指數平滑法
基本方法,加權係數,初始值,預測計算步驟,
基本方法
移動平均法只是利用過去一部分序列來進行預測的，而且用的是算術平均值，即認為起作用的數據點對未來預測值起同等作用。這是不太合理的。為了彌補這些缺點，就產生了指數滑動平均法。指數滑動平均法是時間序列預測中的一種重要方法，也是一種簡單而有效的預測手段。
指數滑動平均法是對整個時間序列進行加權平均的一種方法。加權平均就是每一個已知數據都對未來值貢獻一部分力量。
已知一個時間序列
，它的一次加權平均值
為：
若令
，通過數學論證，則有
以一次指數平滑值為新的時間序列，再一次進行指數平滑，就可得二次指數平滑值
。 ·
如果統計數據有線性變化趨勢，則線性平滑預測公式為：
通過對具有線性關係的數據點進行分析，可以求出平滑係數。
其中：為t周期的一次指數平滑值，為t周期的二次指數平滑值。
在運用公式(3)進行預測時，需要注意兩個問題，一是加權係數的選取，一是初始值的估算。
加權係數
在平滑值公式(1)，(2)中，相當於：
平滑值=(新數據)+(
)(原平滑值)
因為原平滑值與舊數據有關，所以加權係數是新舊數據在平滑中的分配比值。取值的大小，實際上體現了不同時期的數據在預測中所起的不同作用。越大，新數據所起的作用也就越大。若過大，適應新水平過快，靈敏度高，容易對異常現象過敏，過小，比較保守，容易落後於新的發展趨勢。
掌握好值，是用好平滑法預測的重要環節。一般多採用幾個值計算，進行多方案分析。根據實際預測經驗，一般取值在0.01~0.30之間，在實際計算中，可取0.30，0.20、0.10、0.05等幾個數值。
初始值
由(1)式可知，當t=1時，則有
已知統計數據點數是從1開始的，所以
分別為一，二次指數平滑值的初始值。·
指數平滑值就是加權平均值，值的加權作用可用下式說明：
其中：
所以 
繼續以同樣的方式推導，可得
當數據點較多時，如t>10，初始值的作用很小，可以取
當數據點較少時，如t<10，初始值的作用稍大些，這時可以採用前幾個數據點的平均值。
預測計算步驟
1．收集一個時間序列，時間單位可以是年，季，月等。
2．求指數平滑預測方程式。
計算指數平滑值 
，
確定平滑係數 
，
求出指數平滑預測方程式
。
3．進行預測。給定一個時間後，首先確定T值，t為目前的周期數，T為t周期以後需要預測的周期數。根據T值的大小，利用預測方程式，就可以求出
周期的預測值。
