指數平滑法

指數平滑法實際上是一種特殊的加權移動平均法。其特點是: 第一，指數平滑法進一步加強了觀察期近期觀察值對預測值的作用，對不同時間的觀察值所賦予的權數不等，從而加大了近期觀察值的權數，使預測值能夠迅速反映市場實際的變化。權數之間按等比級數減少，此級數之首項為平滑常數a,公比為(1- a)。第二，指數平滑法對於觀察值所賦予的權數有伸縮性，可以取不同的a 值以改變權數的變化速率。如a取小值，則權數變化較迅速，觀察值的新近變化趨勢較能迅速反映於指數移動平均值中。因此，運用指數平滑法，可以選擇不同的a 值來調節時間序列觀察值的均勻程度(即趨勢變化的平穩程度)。

基本介紹

• 中文名：指數平滑法
• 外文名：Exponential Smoothing，ES
• 提出人：布朗
• 基本公式：St=aYt-1+(1-a)St-1
• 學科：統計學

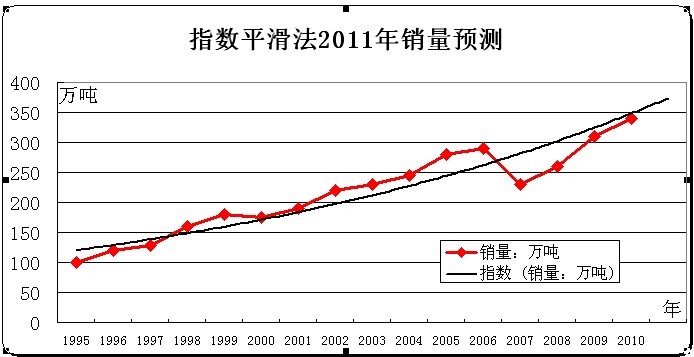
簡介

指數平滑法是生產預測中常用的一種方法。也用於中短期經濟發展趨勢預測，所有預測方法中，指數平滑是用得最多的一種。簡單的全期平均法是對時間數列的過去數據一個不漏地全部加以同等利用；移動平均法則不考慮較遠期的數據，並在加權移動平均法中給予近期資料更大的權重；而指數平滑法則兼容了全期平均和移動平均所長，不捨棄過去的數據，但是僅給予逐漸減弱的影響程度，即隨著數據的遠離，賦予逐漸收斂為零的權數。

也就是說指數平滑法是在移動平均法基礎上發展起來的一種時間序列分析預測法，它是通過計算指數平滑值，配合一定的時間序列預測模型對現象的未來進行預測。其原理是任一期的指數平滑值都是本期實際觀察值與前一期指數平滑值的加權平均。

預測公式

據平滑次數不同，指數平滑法分為：一次指數平滑法、二次指數平滑法和三次指數平滑法等。

一次指數平滑預測

當時間數列無明顯的趨勢變化，可用一次指數平滑預測。

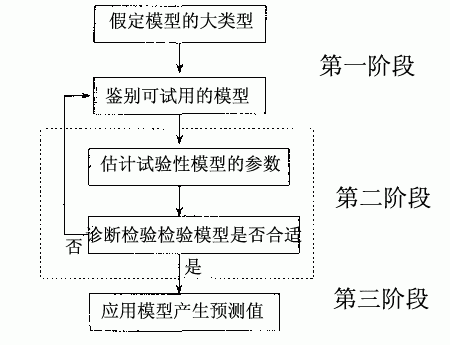一次指數平滑法

其預測公式為：yt+1'=ayt+(1-a)yt' 式中，yt+1'--t+1期的預測值，即本期（t期）的平滑值St ； 　yt--t期的實際值； 　yt'--t期的預測值，即上期的平滑值St-1 。

該公式又可以寫作：yt+1'=yt'+a(yt- yt')。可見，下期預測值又是本期預測值與以a為折扣的本期實際值與預測值誤差之和。

二次指數平滑預測

二次指數平滑是對一次指數平滑的再平滑。它適用於具線性趨勢的時間數列。其預測公式為：

yt+m=(2+am/(1-a))yt'-(1+am/(1-a))yt=(2yt'-yt)+m(yt'-yt) a/(1-a)式中，yt= ayt-1'+(1-a)yt-1 　顯然，二次指數平滑是一直線方程，其截距為：(2yt'-yt)，斜率為：(yt'-yt) a/(1-a),自變數為預測天數。

二次指數平滑基本公式 St=αSt+(1-α)St-1 Yt+T=at+btT at=2St-St bt=(α/1-α)(St-St).

St--第t期的一次指數平滑值；

St-1--第t期的二次指數平滑值；

α--平滑係數 ；

Yt+T--第t+T期預測值 ；

T--由t期向後推移期數

三次指數平滑預測

三次指數平滑預測是二次平滑基礎上的再平滑。

其預測公式是：yt+m=(3yt'-3yt+yt)+[(6-5a)yt'-(10-8a)yt+(4-3a)yt]*am/2(1-a)2+ (yt'-2yt+yt')*a2m2/2(1-a)2 式中，yt=ayt-1+(1-a)yt-1

它們的基本思想都是：預測值是以前觀測值的加權和，且對不同的數據給予不同的權，新數據給較大的權，舊數據給較小的權。

趨勢調整

一段時間內收集到的數據所呈現的上升或下降趨勢將導致指數預測滯後於實際需求。通過趨勢調整，添加趨勢修正值，可以在一定程度上改進指數平滑預測結果。調整後的指數平滑法的公式為：包含趨勢預測(YITt)=新預測（Yt）+趨勢校正（Tt）。

進行趨勢調整的指數平滑預測有三個步驟：

1、 利用前面介紹的方法計算第t期的簡單指數平滑預測（Yt）；

2、 計算趨勢。其公式為： Tt=(1-b)Tt-1+b(Yt-Yt-1)

其中，

Tt=第t期經過平滑的趨勢；

Tt-1=第t期上期經過平滑的趨勢；

b=選擇的趨勢平滑係數；

Yt=對第t期簡單指數平滑預測；

Yt-1=對第t期上期簡單指數平滑預測。

3、計算趨勢調整後的指數平滑預測值（YITt).計算公式為：YITt=Yt+Tt。

套用步驟

模型的建立

指數平滑法一般有一次指數平滑法、二次指數平滑法和三次指數平滑法。指數平滑法的預測模型為：

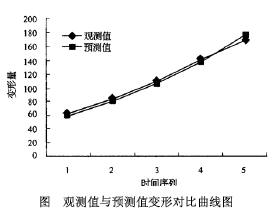指數平滑法在小浪底大壩變形

初始值的確定，即第一期的預測值。一般原數列的項數較多時（大於15項），可以選用第一期的觀察值或選用比第一期前一期的觀察值作為初始值。如果原數列的項數較少時（小於15項），可以選取最初幾期（一般為前三期）的平均數作為初始值。指數平滑方法的選用，一般可根據原數列散點圖呈現的趨勢來確定。如呈現直線趨勢，選用二次指數平滑法；如呈現拋物線趨勢，選用三次指數平滑法。或者，當時間序列的數據經二次指數平滑處理後，仍有曲率時，套用三次指數平滑法。

係數α的確定

指數平滑法的計算中，關鍵是α的取值大小，但α的取值又容易受主觀影響，因此合理確定α的取值方法十分重要，一般來說，如果數據波動較大，α值應取大一些，可以增加近期數據對預測結果的影響。如果數據波動平穩，α值應取小一些。理論界一般認為有以下方法可供選擇：

經驗判斷法。這種方法主要依賴於時間序列的發展趨勢和預測者的經驗做出判斷。

1、當時間序列呈現較穩定的水平趨勢時，應選較小的α值，一般可在0.05～0.20之間取值；

2、當時間序列有波動，但長期趨勢變化不大時，可選稍大的α值，常在0.1～0.4之間取值；

3、當時間序列波動很大，長期趨勢變化幅度較大，呈現明顯且迅速的上升或下降趨勢時，宜選擇較大的α值，如可在0.6～0.8間選值，以使預測模型靈敏度高些，能迅速跟上數據的變化；

4、當時間序列數據是上升（或下降）的發展趨勢類型，α應取較大的值，在0.6~1之間。

試算法。根據具體時間序列情況，參照經驗判斷法，來大致確定額定的取值範圍，然後取幾個α值進行試算，比較不同α值下的預測標準誤差，選取預測標準誤差最小的α。

在實際套用中預測者應結合對預測對象的變化規律做出定性判斷且計算預測誤差，並要考慮到預測靈敏度和預測精度是相互矛盾的，必須給予二者一定的考慮，採用折中的α值。

示例

以某軟體公司A為例，給出2000-2005年的歷史銷售資料，將數據代入指數平滑模型，預測2006年的銷售額，作為銷售預算編制的基礎。

根據經驗判斷法，A公司2000-2005年銷售額時間序列波動很大，長期趨勢變化幅度較大，呈現明顯且迅速的上升趨勢，宜選擇較大的α值，可在0.5～0.8間選值，以使預測模型靈敏度高些，結合試算法取0.5，0.6,0.8分別測試。經過第一次指數平滑後，數列散點圖呈現直線趨勢，故選用二次指數平滑法即可。

根據偏差平方的均值（MSE）最小，即各期實際值與預測值差的平方和除以總期數，以最小值來確定α的取值的標準，經測算當α=0.6時，MSE1=1445.4；當α=0.8時，MSE2=10783.7；當α=0.5時，MSE3=1906.1。因此選擇α=0.6來預測2006年4個季度的銷售額。