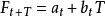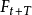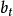指數平滑預測法

指以某種指標的本期實際數和本期預測數為基礎，引入一個簡化的加權因子，即平滑係數，以求得平均數的一種時間序列預測法。即對離預測期較近的歷史數據給予較大的權數，權數由近到遠按指數規律遞減的一種特殊的加權平均法。

基本介紹

• 中文名：指數平滑預測法
• 外文名：Exponential smoothing prediction method
• 學科：數學
• 套用：統計預測
• 提出者：布朗
• 隸屬：時間序列預測法

基本內容

時間序列是指同一變數按事件發生的先後順序排列起來的一組觀察值或記錄值。構成時間序列的要素有兩個：其一是時間，其二是與時間相對應的變數水平。 實際數據的時間序列能夠展示研究對象在一定時期內的發展變化趨勢與規律，因而可以從時間序列中找出變數變化的特徵、趨勢以及發展規律，從而對變數的未來變化進行有效地預測。

時間序列預測法的基本特點是：假定事物的過去趨勢會延伸到未來；預測所依據的數據具有不規則性；撇開了市場發展之間的因果關係。

時間序列預測的主要方法：平均（平滑）預測法、長期趨勢預測法、季節變動預測法、指數平滑預測法。

產生背景：指數平滑由布朗提出，他認為時間序列的態勢具有穩定性或規則性，所以時間序列可被合理地順勢推延；他認為最近的過去態勢，在某種程度上會持續的未來，所以將較大的權數放在最近的態勢。

基本原理：指數平滑法是移動平均法中的一種，其特點在於給過去的觀測值不一樣的權重，即較近期觀測值的權數比較遠期觀測值的權數要大。根據平滑次數不同，指數平滑法分為一次指數平滑法、二次指數平滑法和三次指數平滑法等。但它們的基本思想都是：預測值是以前觀測值的加權和，且對不同的數據給予不同的權數，新數據給予較大的權數，舊數據給予較小的權數。

分類

據平滑次數的不同，指數平滑預測法可以分為：一次指數平滑預測法、二次指數平滑預測法、高次指數平滑預測法。

一次指數平滑預測法

當時間數列無明顯的趨勢變化，可用一次指數平滑預測。其預測公式為： 。

--t+1期的預測值，即本期（t期）的平滑值St ；
yt--t期的實際值；
yt--t期的預測值，即上期的平滑值St-1 。

指數平滑法初始值的確定

從時間序列的項數來考慮：若時間序列的觀察期n大於15時，初始值對預測結果的影響很小，可以方便地以第一期觀測值作為初始值；若觀察期n小於15，初始值對預測結果影響較大，可以取最初幾期的觀測值的平均數作為初始值，通常取前3個觀測值的平均值作為初始值。

一次指數平滑法的特點
1.調整預測值的能力強。
2.預測值包含的信息量是全部歷史數據。
3.加權的特點是離預測期較近的權數較大，較遠的權數較小。權數之和為1。

二次指數平滑預測法

一次指數平滑法的局限性：一次指數平滑法只適用於水平型歷史數據的預測，不適用於呈斜坡型線性趨勢歷史數據的預測。
解決步驟：
1.先求出一次指數平滑值和二次指數平滑值的差值；
2.將差值加到一次指數平滑值上；
3.再考慮趨勢變動值。

為t+T期的預測值；T為t期到預測期的間隔期數； 、 為參數。

三次指數平滑預測法

若時間序列的變動呈現出二次曲線趨勢，則需要採用三次指數平滑法進行預測。三次指數平滑是在二次指數平滑的基礎上再進行一次平滑，其計算公式為 。

平滑係數的選擇

在指數平滑法中，預測成功的關鍵是 的選擇。 的大小規定了在新預測值中新數據和原預測值所占的比例。 值愈大，新數據所占的比重就愈大，原預測值所占比重就愈小，反之亦然。

①當時間序列呈穩定的水平趨勢時，α應取較小值，如0.1～0.3；
②當時間序列波動較大，長期趨勢變化的幅度較大時，α應取中間值，如0.3～0.5；
③當時間序列具有明顯的上升或下降趨勢時，α應取較大值，如0.6～0.8；

在實際運用中，可取若干個α值進行試算比較，選擇預測誤差最小的α值。

優缺點

指數平滑預測法的優點

（1）對不同時間的數據的非等權處理較符合實際情況。
（2）實用中僅需選擇一個模型參數，即可進行預測，簡便易行。
（3）具有適應性，也就是說預測模型能自動識別數據模式的變化而加以調整。

指數平滑預測法的缺點

（1）對數據的轉折點缺乏鑑別能力，但這一點可通過調查預測法或專家預測法加以彌補。

（2）長期預測的效果較差，故多用於短期預測。

套用舉例

下期預測數=本期預測數+ 平滑係數（本期實際數- 本期預測數）這個公式的含義是：在本期預測數上加上一部分用平滑係數調整過的本期實際數與本期預測數的差，就可求出下期預測數。一般說來，下期預測數常介乎本期實際數與本期預測數之間。平滑係數的大小，可根據過去的預測數與實際數比較而定。差額大，則平滑係數應取大一些；反之，則取小一些。平滑係數愈大，則近期傾向性變動影響愈大；反之，則近期的傾向性變動影響愈小，愈平滑。這種預測法簡便易行，只要具備本期實際數、本期預測數和平滑係數三項資料，就可預測下期數。例如某種產品銷售量的平滑係數為0.4，1996年實際銷售量為31萬件，預測銷售量為33萬件。則1997年的預測銷售量為：1997年預測銷售量= 31萬件×0.4+33萬件×（1-0.4）=32.2萬件。