基本介紹
- 中文名:指數不等式
- 外文名:exponential inequality
- 所屬學科:數學
- 相關概念:指數函式,指數,對數,單調性等
基本介紹
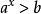
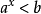
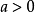

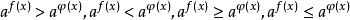



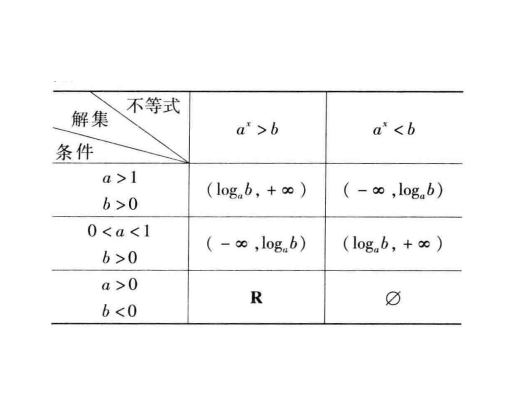
指數不等式的解法
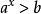
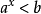
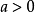

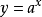

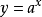
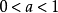
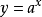
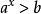




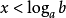

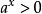
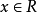
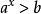 | 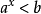 | |
 |  |  |
 |  | 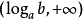 |
 | 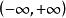 | 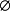 |







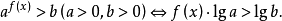


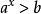
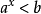
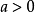

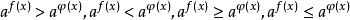



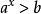
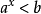
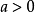

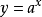

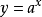
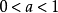
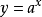
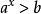




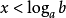

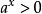
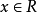
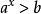 | 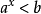 | |
 |  |  |
 |  | 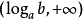 |
 | 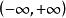 | 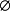 |







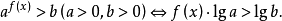


指數中含有未知數的不等式叫指數不等式。指數不等式解法的主要思想是:根據不等式的基本性質,並利用指數函式和對數函式的單調性求得其解,或是轉化為代數不等式再...
簡單指數不等式(simple exponential inequality)亦稱最簡指數不等式,是一種常見的指數不等式,即形如ax0,a≠1),ax>b(a>0,a≠1)的不等式。...
萬有范指數不等式(universal norm index in-equation )亦稱(或相當於)第二不等式.類域論的重要不等式.若K/k為n次伽羅瓦擴張,m是數域k的一個模,含所有分歧...
《不等式研究(第2輯)》收集了全國不等式研究專家、學者最新的不等式研究成果,涉及分析不等式研究,高等幾何不等式研究,初等不等式研究,數學套用研究以及一些不等式...
《不等式探究》是2016年出版的圖書,作者是安振平。...... 本書共四篇,包括:兩數和與積的不等關係,課本條件指數不等式的探究,一個不等式的化筒,溝通兩個經典問...
琴生不等式以丹麥技術大學數學家約翰·延森(Johan Jensen)命名。它給出積分的凸函式值和凸函式的積分值間的關係。琴生(Jensen)不等式(也稱為詹森不等式),使用時...
,通過極限過程不難得到級數形式的赫爾德不等式從基本(或二重)赫爾德不等式(2) 與(4)出發,可以得到多重赫爾德不等式。定理3 設 是一組共軛指數,即 ,設 是 列...
莫爾斯不等式簡介 編輯 在數學中,特別是在差分拓撲中,莫爾斯理論使得人們可以...小函式的干擾,則擾動函式在非擾動函式的臨界流形上的所有關鍵點的指數將位於i...
在物理學和數學上,高登─湯普森不等式(Golden–Thompson inequality)是一個由Golden (1965)和Thompson (1965)二氏所證明的不等式,此不等式在統計力學上相當重要,而...
