拋物線拱(parabolic arch)是幾何學術語,指工程建築上常用的一種拱形,例如橋拱,它的拱軸線比較理想的是採用懸鏈線y=a(e+e)/2,拋物線只是它的一種近似曲線。
基本介紹
- 中文名:拋物線拱
- 外文名:parabolic arch
- 所屬學科:數學
- 所屬問題:平面解析幾何
基本介紹

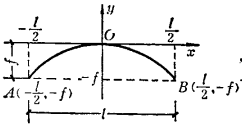
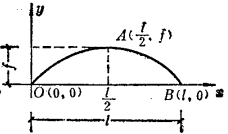







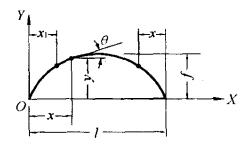

例題解析
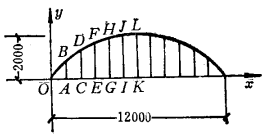



拋物線拱(parabolic arch)是幾何學術語,指工程建築上常用的一種拱形,例如橋拱,它的拱軸線比較理想的是採用懸鏈線y=a(e+e)/2,拋物線只是它的一種近似曲線。
















拋物線拱(parabolic arch)是幾何學術語,指工程建築上常用的一種拱形,例如橋拱,它的拱軸線比較理想的是採用懸鏈線y=a(ex/a+e-x/a)/2,拋物線只是它的一種近似曲線。基本介紹所謂拋物線拱,就是由拋物...
拋物線拱壩 我國已建各種形式大小拱壩800餘座,然而已建拋物線拱壩只有3座:貴州東風拱壩、台灣斐翠拱壩和四川二灘拱壩。拋物線型雙曲拱壩設計技術先進,已成為當前水利水電工程混凝土大壩首選壩型之一。拋物線型雙曲拱壩的坐標計算,是要解決拱壩體型控制以及模板(或混凝土)偏差檢測問題;
主要研究內容、重要結果和關鍵數據如下: (1)通過三種不同矢跨比鋼管混凝土拋物線拱在三種不同荷載工況下的試驗研究,得到了在均布豎向荷載和四分點荷載作用下,鋼管混凝土拋物線拱的平面內失穩破壞模式為反對稱失穩;在拱頂載入工況下,鋼管混凝土拋物線拱則呈現出正對稱的失穩破壞模式。鋼管混凝土拋物線拱平面內...
系拱曲線方程分為直線型、拋物線型、直線接曲線(拋物線或圓曲線)型,各種曲線方程的適用範圍如下:(1)直線型系拱多用於剛性路面,如水泥混凝土路面和大型預製塊鋪裝路面,也可用於區間窄路和單向排水的非機動車道。(2)拋物線系拱根據橫坡度和路寬的不同採用不同的方次,適用於寬度不超過20m的柔性路面,可以根據攤鋪...
梁拱的形狀有拋物線型,也有折線型。折線型既有單折線型,也有雙摺線型。對於普通商用船舶,標準梁拱高度為型寬的1/50。甲板梁拱還可提供一定的浮力儲備,也可以增加一定的艙容,但也存在不利的一面,即它給甲板機械和設備安裝帶來了不便。圖1為幾種常見的甲板梁拱形狀。圖1中,B為型寬,H為梁拱高度,K.L...
工程中常用的拱有三鉸拱(圖1a)、兩鉸拱(圖1b)和無鉸拱(圖1c)三種。拱的軸線可以是圓弧、拋物線、懸鏈線等。在內力分析中,三鉸拱屬於靜定結構;兩鉸拱屬於一次靜不定結構;無鉸拱屬於三次靜不定結構。後兩者可用力法進行分析。在外載荷作用下,拱一般以受壓為主,因此,除內力和變形外,還須作穩定...
塌落拱是坑硐頂部圍岩失去平衡所形成的拱形塌落圈。拱圈內塌落岩體的質量等於作用於人工襯砌工程之上的山岩壓力。塌落拱可分為自然拱和壓力拱。鬆軟岩石生成的壓力拱為拋物線形。 [1] 中文名 塌落拱 外文名 collapse arch 學科 工程地質學 參考資料 1 http://www.gsdkj.net/pro/view.asp?id=3438 V百...
1.2 三鉸拱 1.3 無鉸拱 1.4 兩鉸拱 本章小結 參考文獻 第二章 拱的平面彎曲屈曲 2.1 曲桿的平面彎曲 2.2 圓拱的平面屈曲 2.3 非圓拱的平面屈曲 2.4 拱的計算長度 2.5 扁拱的平面屈曲 本章小結 參考文獻 第三章 拱的平面振動 3.1 圓拱的平面振動 3.2 拋物線拱的平面振動 3.3 反對稱...
路拱(crown)即路面的橫向斷面做成中央高於兩側,具有一定坡度的拱起形狀。路面表面做成直線或拋物線型,其作用是利用路面橫向排水。是擴建和改建的快速路、主幹路、次幹路及支路機動車道與非機動車道一般路段的路拱橫坡和路拱曲線設計。基本定義 道路橫斷面上路面做成中央高兩側低,具有一定坡度的拱起形狀。其作用是利於...
鐵路路拱,即鐵路線路的橫向斷面做成中央高於兩側,具有一定坡度的拱起形狀。路面表面做成直線或拋物線型,其作用是利用鐵路橫向排水。是擴建和改建的快速鐵路、主幹鐵路、次乾鐵路及支路的路拱橫坡。簡介 鐵路橫斷面做成中央高兩側低,具有一定坡度的拱起形狀。其作用是利於鐵路面橫向排水。鐵路面兩側的坡度稱為鐵路拱橫坡...
川治壩位於日本櫪木縣鹽谷郡、利根川水系(Tonegawa)支流鬼怒川上。混凝土拋物線拱壩,最大壩高140m,水庫總庫容0.83億立方米。工程目的為防洪、保護東京地區約500平方公里免受洪水襲擊、兼有灌溉、城市供水和工業用水功能。1970年開工,1981年竣工。簡介 壩址約100m範圍內兩岸河谷陡峭。高程590m以下,谷坡坡角約70...
拱形有半圓、多邊形、圓弧、橢圓、拋物線、蛋形、馬蹄形和尖拱形,可說應有盡有。孔數上有單孔與多孔,多孔以奇數為多,偶數較少,多孔拱橋,如果當某孔主拱受荷時,能通過橋墩的變形或拱上結構的作用將荷載由近及遠的傳遞到其它孔主拱上去,這樣的拱橋稱為連續拱橋,簡稱連拱;江浙水鄉的三、五、七、九孔石...
③將拱端向岸壁深挖嵌進,以擴大下游的抗滑岩體,也可避開不利的滑裂面。這種做法對增加拱座的穩定性較有效。④改進拱圈設計,如採用三心拱、拋物線拱等形式,使拱端推力儘可能趨向正交於岸坡。⑤如拱端基岩承載能力較差,可局部擴大拱端或設定推力墩。特殊構造 拱壩的若干特殊構造 (一)墊座 墊座設定在拱壩壩體...
7.2.2求解超靜定兩鉸拱的解析方法 7.2.3求解超靜定無鉸拱的解析方法 7.2.4超靜定拱的反力及內力計算方法 7.2.5軸向變形的影響 7.3任意外形對稱三鉸拱 7.4超靜定圓弧拱 7.4.1圓弧拱拱軸幾何數據 7.4.2相關計算理論與係數 7.4.3各種荷載作用下的贅餘力計算公式 7.5超靜定變截面拋物線拱 7....
路拱區即路面的橫向斷面做成中央高於兩側,具有一定坡度的拱起形狀。路面表面做成直線或拋物線型,其作用是利用路面橫向排水。是擴建和改建的快速路、主幹路、次幹路及支路機動車道與非機動車道一般路段的路拱區橫坡和路拱區曲線設計。基本形式一次式:直線形、折線形二次式:拋物線形,線形方程為 y=(h1/B)*X+(2h1/...
減少岩體內的滲流壓力。(3)將拱端向岸壁深挖嵌進,以擴大下游的抗滑岩體,也可避開不利的滑裂面。這種做法對增加拱座的穩定性較為有效。(4)改進拱圈設計,如採用三心拱、拋物線拱等型式,使拱端推力儘可能轉向正交於岸坡。(5)如拱端基岩承載能力較差,可局部擴大拱端或設定重力墩。
20. 何星、李章政、於建華,一座斜拉橋的健康檢測與計算分析,四川建築,No.3 Vol,2000,第35-36頁。【12】李章政、熊 峰,等截面拋物線拱的彈性回響分析,四川建築,第20卷增刊,2000,第212-215頁。21. 魏潔、李章政,錯列桁架結構體系的靜力彈塑性分析,建築技術開發,2005,第1期。22. 楊英雄、李章政、...
拱形可以是平面的也可以是立體的,拱形可以是圓或圓柱體的一部分,有時球形的一部分也算,也可以是拋物線、橢圓的一部分。拱形受壓時會把這個力傳給相鄰的部分抵住拱足散發的力就可以承受更大的壓力。所以拱形所能承受的力量更重。名詞解釋 兩個半球形可以組合成一個球形,球形也可以看成是若干個拱形的組合,球形...
主拱圈 主拱圈,拱橋上部結構中兩端支承在墩台上、呈曲線形向上拱起的主要承重結構。承受橋上的作用載荷,並把載荷傳遞給橋墩、橋台。常用軸線形式有圓弧線、拋物線和懸鏈線。橫截面形式有整體或分離的板拱、兩個以上分離的肋拱和箱形拱等。按所用材料,分圬工(磚、石或素混凝土)拱圈、鋼筋混凝土拱圈和鋼拱圈等。
圖1為磚拱結構套用實例。拱按採用材料的不同分為土拱、木拱、磚石拱、混凝土拱、鋼筋混凝土拱、鋼拱等。按採用拱軸的線型的不同分為圓弧拱、拋物線拱、懸鏈線拱等。按所含鉸的數目的不同分為三鉸拱、雙鉸拱和無鉸拱。按拱圈截面形式的不同可分為實體拱、箱形拱和桁架拱等。拱腳 拱腳是拱頂的基礎,是拱頂...
