人物生平 早年生活,砥礪人生
1646年7月1日,戈特弗里德·威廉·萊布尼茨出生於
神聖羅馬帝國 的
萊比錫 ,祖父三代人均曾在薩克森政府供職,父親是Friedrich Leibnütz,母親是Catherina Schmuck。長大後,萊布尼茨名字的
拼法 才改成“Leibniz”,但是一般人習慣寫成“Leibnitz”。晚年時期,他的簽名通常寫成“von Leibniz”,以示貴族身份。萊布尼茨死後,他的作品才公布於世,作者名稱通常是“Freiherr [
Baron ] G. W. von Leibniz.”,但沒有人確定他是否確實有男爵的貴族頭銜。
萊布尼茨的父親是
萊比錫大學 的倫理學教授,在萊布尼茨6歲時去世,留下了一個私人的圖書館。12歲時自學
拉丁文 ,並著手學習
希臘文 。14歲時進入萊比錫大學念書。20歲時完成學業,專攻法律和一般大學課程。1666年他出版第一部有關於哲學方面的書籍,書名為《論組合術》(de arte combinatoria)。
任職法庭,鏖戰法壇
1666年萊布尼茨於Altdorf拿到博士學位後,拒絕了教職的聘任,並經由當時政治家Boineburg男爵的介紹,任職服務於美茵茨
選帝侯 大主教Johann Philipp von Schönborn的高等法庭。
萊布尼茨
1671年發表兩篇論文《抽象運動的理論》(Theoria motus abstracti)及《新物理學假說》(Hypothesis physica nova),分別題獻給巴黎的科學院和
倫敦 的
皇家學會 ,在當時歐洲學術界增加了知名度。
1672年萊布尼茨被Johann Philipp派至
巴黎 ,以動搖
路易十四 對入侵
荷蘭 及其它
西歐 日耳曼 鄰國的興趣,並轉投注精力於埃及。這項政治計畫並沒有成功,但萊布尼茨卻進入了巴黎的知識圈,結識了
馬勒伯朗士 和數學家惠更斯等人。這一時期的萊布尼茨特別研究數學,而發明了
微積分 。
1672及1673年Boineburg和Johann Philipp卻相繼過世,迫使萊布尼茨最後於1676年離開巴黎而轉任職服務於
漢諾瓦 的Johann Friedrich公爵。於上任時,順道于海牙拜訪
斯賓諾莎 ,與其數天一同討論哲學。之後萊布尼茨就到漢諾瓦管理圖書館,並擔任公爵法律顧問。
1679年,萊布尼茨發明了
二進制 ,並對其系統性深入研究,完善了二進制。
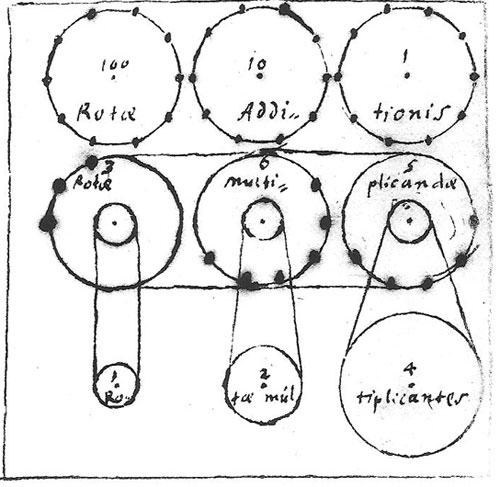
萊布尼茨設計的計算器運行簡圖
1680至1685年間,擔任
哈茨山 銀礦 礦采工程師。在這期間,萊布尼茨致力於風車設計,以抽取礦坑中的地下水。然而受限於技術問題和礦工
傳統觀念 的阻力,計畫沒有成功。
1685年起,再受繼任的公爵Ernst August所託,轉而開始做其Braunschweig-Lüneburg貴族族譜研究。這項計畫一直到萊布尼茨去世前都沒有完成。
1686年完成《形上學論》(Discours de métaphysique)。
1689年為完成Braunschweig-Lüneburg族譜研究,遊歷於
義大利 。其時結識耶穌會派遣於中國的傳教士,而開始對中國事物有更強烈的興趣。
1695年於期刊發表《新系統》,進而使萊布尼茨哲學中,關於實體間與心物間之“
預定和諧 ”理論,被廣泛認識。
擔任院長,拒絕倫敦
1700年萊布尼茨說服
布蘭登堡選帝侯 腓特烈三世於柏林成立科學院,並擔任首任院長。
1704年完成《
人類理智新論 》。本文針對洛克的《人類理智論》,用對話的體裁,逐章節提出批評。然因洛克的突然過世,萊布尼茨不願被落入欺負死者的口實,所以本書在萊布尼茨生前一直都沒有出版。
1710年,出於對1705年過世的普魯士王后Sophie Charlotte的感念,出版《神義論》(Essais de Théodicée)。
1714年於
維也納 著寫《
單子論 》(La Monadologie;標題為後人所加)及《建立於理性上之自然與恩惠的原理》。同年,漢諾瓦公爵Georg Ludwig繼任為
英國國王 喬治一世 ,卻拒絕將萊布尼茨帶至倫敦,而將他疏遠於漢諾瓦。
晚年逝世
1716年11月14日萊布尼茨於
漢諾瓦 孤獨地過世,除了他自己的秘書外,即使George Ludwig本人正巧在
漢諾瓦 ,宮廷無其他人參加他的喪禮。直到去世前幾個月,才寫完一份關於中國人
宗教思想 的手稿:《論中國人的自然神學》。
人物成就 微積分 萊布尼茨與
艾薩克·牛頓 誰先發明
微積分 的爭論是數學界至今最大的公案。萊布尼茨於1684年發表第一篇微分論文,定義了微分概念,採用了
微分符號 dx、dy。1686年他又發表了積分論文,討論了微分與積分,使用了
積分符號 ∫。依據萊布尼茨的筆記本,1675年11月11日他便已完成一套完整的
微分學 。
萊布尼茨
然而1695年英國學者宣稱:微積分的
發明權 屬於
艾薩克·牛頓 ;1699年又說:
牛頓 是微積分的“第一發明人”。1712年
英國皇家學會 成立了一個委員會調查此案,1713年初發布公告:“確認
艾薩克·牛頓 是微積分的第一發明人。”萊布尼茨直至去世後的幾年都受到了冷遇。由於對牛頓的盲目崇拜,英國學者長期固守於牛頓的
流數 術,只用牛頓的流數符號,不屑採用萊布尼茨更優越的符號,以致英國的數學脫離了數學發展的時代潮流。
不過萊布尼茨對牛頓的評價非常高,在1701年柏林宮廷的一次宴會上,
普魯士國王 腓特烈詢問萊布尼茨對牛頓的看法,萊布尼茨說道:“在從世界開始到牛頓生活的時代的全部數學中,牛頓的工作超過了一半。”
牛頓 在1687年出版的《
自然哲學的數學原理 》的第一版和第二版也寫道:“十年前在我和最傑出的幾何學家萊布尼茨的通信中,我表明我已經知道確定
極大值 和
極小值 的方法、作
切線 的方法以及類似的方法,但我在交換的信件中隱瞞了這方法,……這位最卓越的科學家在回信中寫道,他也發現了一種同樣的方法。他並訴述了他的方法,它與我的方法幾乎沒有什麼不同,除了他的措詞和符號而外”(但在第三版及以後再版時,這段話被刪掉了)。因此,後來人們公認牛頓和萊布尼茨是
各自獨立 地創建微積分的。
萊布尼茨紀念郵票
牛頓 從物理學出發,運用幾何
方法研究 微積分,其套用上更多地結合了
運動學 ,造詣高於萊布尼茨。萊布尼茨則從幾何問題出發,運用
分析學 方法引進微積分概念、得出
運算法則 ,其數學的嚴密性與系統性是牛頓所不及的。
萊布尼茨認識到好的
數學符號 能節省思維勞動,運用符號的技巧是數學成功的關鍵之一。因此,他所創設的微積分符號遠遠優於牛頓的符號,這對微積分的發展有極大影響。1714至1716年間,萊布尼茨在去世前,起草了《微積分的歷史和起源》一文(本文直到1846年才被發表),總結了自己創立微積分科學的思路,說明了自己成就的獨立性。
拓撲學 拓撲學 最早稱之“位相分析學”(analysis situs),是萊布尼茨1679年提出的,這是一門研究地形、地貌相類似的學科,當時主要研究的是出於數學分析的需要而產生的一些幾何問題。關於萊布尼茨對拓撲學的貢獻,尚存爭論。Mates引用Jacob Freudenthal1954年一篇論文裡的話說:
儘管萊布尼茨認為一列點在空間中的位置是由其間距離唯一決定的——
若且唯若 距離發生變化時點的位置發生相應的改變——他的仰慕者
歐拉 ,在他著名的一篇論文(1736年發表,解決了哥尼斯堡(
加里寧格勒 )
七橋問題 及其推廣)中,卻是在“
拓撲 變形時點的位置不發生變化”的意義下使用“幾何位置”這個名詞的。他誤信了萊布尼茨是這個概念的創始者。……人們常常意識不到萊布尼茨是在完全不同的意義下使用這個名詞的,因此被尊為數學的這個分支領域的奠基人並不恰當。
在萊布尼茨海量的
科學成果 中探索是發人深省的體驗。除了微積分以及其他已經完成的研究之外,大量涉及內容廣泛且極富前瞻性的研究對科學發展的
推動力 勢不可擋。在‘填充理論’上即有例子,……在發現萊布尼茨還曾經關注過
幾何度量 的重要性之後,我對他的狂熱更甚了。在“
歐幾里德 普羅塔”中……,其使得歐幾里德公理更加嚴格,他陳述道,……‘對直線,我有數種不同的定義。直線是曲線的一種,而曲線的任何部分都是和整體相似的,因此直線也具有這種特性;這不僅適用於曲線,而且適用於集合。’這個論斷今天已經可以被證明。
因而
分形幾何 (由
本華·曼德博 發揚光大)理論在萊布尼茨的
自相似性 思想和
連續性原理 中尋求支持:大自然沒有跳躍(
拉丁語 “natura non facit saltus”,英語"nature does not make jumps")。當萊布尼茨在他的《形上學論》著作中寫道,“直線是曲線的一種,其任何部分都是和整體類似的”,他實際上提前兩個世紀預言了拓撲學的誕生。至於“填充理論”,萊布尼茨對他的朋友Des Bosses說,“你想像一個圓,然後用三個全等的最大半徑的圓填滿它,後來的三個小圓又可以以同樣的過程被更小的圓填充”。這個過程可以無限地繼續下去,並由此生髮出了自相似性的思想。萊布尼茨對於歐氏公理的改進亦包含同樣的概念。
符號思維 萊布尼茨有個顯著的信仰,大量的人類推理可以被
歸約 為某類運算,而這種運算可以解決看法上的差異:
“精煉我們的推理的唯一方式是使它們同數學一樣切實,這樣我們能一眼就找出我們的錯誤,並且在人們有爭議的時候,我們可以簡單地說:讓我們計算[calculemus],而無須進一步的忙亂,就能看出誰是正確的。”(發現的藝術 1685,W 51)
萊布尼茨的演算推論器,很能讓人想起
符號邏輯 ,可以被看作使這種計算成為可行的一種方式。萊布尼茨寫的備忘錄(帕金森1966年翻譯了它們)可以被看作是對符號邏輯的探索——所以他的演算——上路了。但是Gerhard和Couturat沒有出版這些著作,直到現代
形式邏輯 在19世紀80年代於Frege的概念文字和Charles Peirce及他的學生的著作中形成,所以就更在
喬治·布爾 和
德·摩根 在1847開創這種邏輯之後了。
單子論 除了是一位出眾的天才數學家之外,萊布尼茨亦是
歐陸理性主義 哲學的高峰。承繼了
西方哲學 傳統的思想,他認為世界,因其確定(換句話說,有關世界的知識是客觀普遍和必然的)之故,必然是由自足的實體所構成。所謂的自足,是不
依他 物存在和不依他物而被認知。萊布尼茨的前輩
巴魯赫·斯賓諾莎 以為實體只有一個,就是神/自然。萊布尼茨對此不敢苟同,原因之一是斯氏的泛神觀和聖經的神學有明顯衝突,其次,是因為斯氏的理論沒有能夠解決由
笛卡兒 以降的
二元論 ,令世界出現了斷層(他雖然強調世界為一,但沒有說明這一個看來是
二元對立 的世界的一統是如何可能)。
萊布尼茨以為實體是多的,是無限多的。跟隨
亞里士多德 的實體觀,他以為實體是一命題的主語。在一個命題S是P中,S就是實體。因為實體是自足的,則它要包含所有可能的謂語,即是“...是P”。由此,我們可以推出,實體有四個特徵:不可分割性、
封閉性 、統有性和道德性。
不可分割性是指,任何有
廣延 的東西,即有長度的東西,都可以被分割。被分割了的東西分別包含了自己的全部可能性,並且自足,則有廣延的東西的內容,即可能性要依附於他的部分的可能性。如此類推,則只要有廣
延性 ,就不自足,而要依他物而被知(對萊布尼茨來說,真正的知識就是要窮一物的可能性),就不是實體。故實體不可分割,是一沒有廣延的東西,在萊布尼茨的晚年著作中(Monadology),他稱之為單子(Monad),單子的性質就是思(
thought )。這廣延的世界就是由無限多的單子構成。
封閉性是說每一單子必然是自足的,不依他而存在,而又包含了自己的全部可能性。則一單子不可能和另一單子有
互動作用 (interaction)。若一單子作用於另一單子,則後一單子有一可能性沒有包括在該單子之內,即該單子沒能自足的包含自己的全部內容,而要依附於他物。因為實體的定義,這是不可能的。故萊布尼茨說:“單子之間沒有窗戶。”
統有性是指每一單子都必然以某種角度(perspective)包括了全世界。因為世界是緊密的由因果所構成,故A作用於B,其實不單單是作用於B,而是全世界。如果說一單子的內容包括自身的全部可能,則每一單子均以該單子自身為中心指向全世界。而這個世界是一統的,不等於說所有單子都是一樣的,因為同一世界可以不同的角度來認知,而不失為一一統的世界。
最後,單子的道德性則較複雜。這個特性的提出是基於兩個理由,一、是世界的一統性(unity),二、是世界的
確定性 。對於前者,所有的單子都包含全世界,但各以自己的角度,世界的一統性是不是假的呢?如果我們要說一統,可以如何說起呢?對於後者,世界是由單子構成,單子只是其可能性的集合,世界亦只是一可能。那我們是不是不可能有一種不僅僅是可能,而是必然的知識呢?我們可以在什麼意義下說有關世界的知識是真的、確定的呢?萊布尼茨將之歸功於一神,世界的創造者。從一個方面說,神在創造之前,沒有已成的材料,故沒有既成的有限處境,則創造是一純意志的創造,神是單憑其至善而創造這一個世界的。
故此,如萊布尼茨的名言,這一個確切成就了的世界是“眾多可能的世界之中最好的一個”。這乎合了萊布尼茨的信仰要求。另一方面,要確定的了解一事物,則要了解其原因。要理解這一個原因,又要追索該原因的原因。如此類推,則世界的確定性知識不可能是一世界之內的動因(efficient cause),而是一超越的形上因(metaphysical cause)。
萊布尼茨稱這個理論上必要設定的形上因為神。故,這一個世界之所以是如此,就是因為這是最好的,是至善的
可能世界 。人,要完全理解這神的至善意志,是不可能的,但可朝這一個方向邁進,因為人的心靈作一特殊的單子,是有記憶的,可以基於過去,疇劃自己的未來,這是人類分享的神性,即道德的可能性。人可以透過開放可能性,了解這個神創造的世界,而了解如何成為一個道德的人。
這一種世界的
道德觀 ,可以被視為
康德 的先驅,分別在於萊布尼茨獨斷的提出了神為道德的完滿,把可能性說成了是在神的目光之下的實在,而沒有真正的將世界的可能性看作為可能性。而且萊布尼茨對
天賦觀念 (innate idea)的批評,正是
黑格爾 對
康德 的批評,在這個意義上說,
康德 一方面是被
休謨 (Hume)從萊布尼茨的獨斷夢中喚醒,可是同時亦到由洛克(Locke)起的哲學病變--對理性界限的審查--所污染。在這一方面,萊布尼茨卻比康德走前了一步。
形式邏輯 萊布尼茨是在
亞里士多德 和1847年喬治·布爾和德·摩根分別出版開創現代形式邏輯的著作之間最重要的
邏輯學家 。萊布尼茨闡明了合取、析取、否定、同一、集合包含和
空集 的首要性質。萊布尼茨的
邏輯原理 和他的整個哲學可被歸約為兩點:
所有的我們的觀念(概念)都是由非常小數目的簡單觀念複合而成,它們形成了人類思維的字母。
複雜的觀念來自這些簡單的觀念,是由它們通過模擬
算術運算 的統一的和對稱的組合。
人物軼事 萊布尼茨是最早接觸
中華文化 的歐洲人之一,從一些曾經前往中國傳教的教士那裡接觸到
中國文化 ,之前應該從
馬可·波羅 引起的東方熱留下的影響中也了解過中國文化。法國
漢學 大師若阿基姆·布韋(Joachim Bouvet,漢
名白 晉,1662-1732年)向萊布尼茨介紹了《
周易 》和八卦的系統。在萊布尼茨眼中,“陰”與“陽”基本上就是他的
二進制 的中國版。他曾斷言:“二進制乃是具有世界
普遍性 的、最完美的邏輯語言”。如今在德國
圖林根 ,著名的郭塔王宮圖書館(Schlossbibliothek zu Gotha)內仍保存一份萊氏的手稿,標題寫著“1與0,一切數字的神奇淵源。”
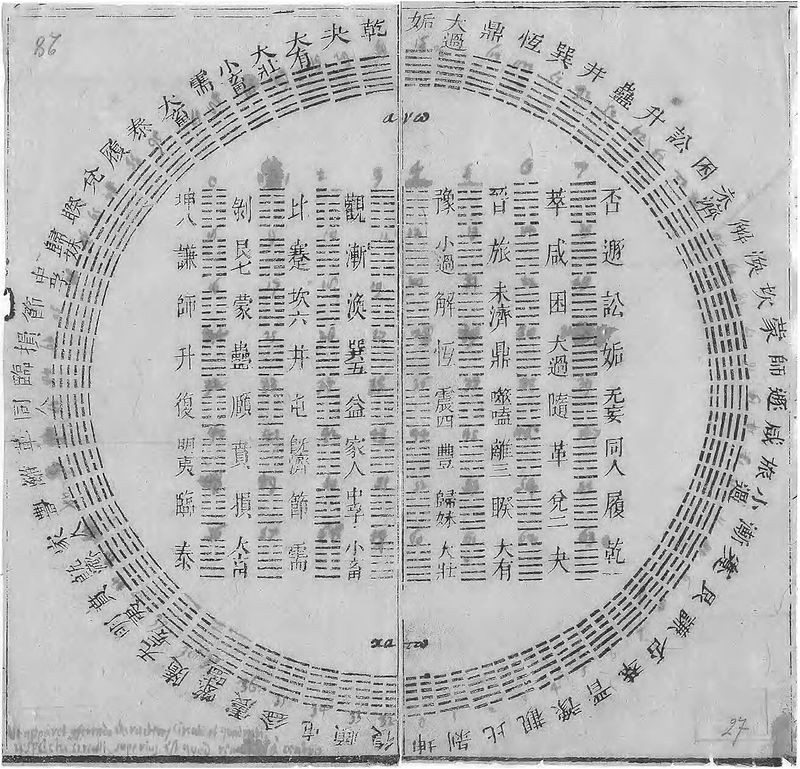
1701年白晉給萊布尼茨的周易圖
其手稿標題全文是:“1與0,一切數字的神奇淵源。……這是造物的秘密美妙的典範,因為,一切無非都來自上帝。”而且萊布尼茨自己寫給若阿基姆·布韋的信中說:“第一天的伊始是1,也就是上帝。第二天的伊始是2,……到了第七天,一切都有了。所以,這最後的一天也是完美的。因為,此時世間的一切都已經被創造出來了。因此它被寫作‘7’,也就是‘111’(二進制中的111等於十進制的7),而且不包含0。只有當我們僅僅用0和1來表達這個數字時,才能理解,為什麼第七天才完美,為什麼7是神聖的數字。特別值得注意的是它(第七天)的特徵(寫作二進制的111)與三位一體的關聯。”
郭書春 在《
古代世界數學泰斗劉徽 》一書461頁中稱:“中國有所謂《周易》創造了二進制的說法,至於萊布尼茲受《周易》八卦的影響創造二進制並用於計算機的神話,更是廣為流傳。事實是,萊布尼茲先發明了二進制,後來才看到傳教士帶回的宋代學者重新編排的《周易》八卦,並發現八卦可以用他的二進制來解釋。”以此為由,認為並不是萊布尼茨看到
陰陽八卦 才發明二進制。梁宗巨著《數學歷史典故》(1995年出版)一書14~18頁對這一歷史公案亦有此說。
胡陽、李長鐸在《萊布尼茨發明二進制前沒有見過先天圖嗎——對歐洲現存17世紀中西交流文獻的考證》通過對歐洲現存17世紀中西交流文獻的研究考證,否定了萊布尼茨在發明二進制以後才見到先天圖的說法。先天圖在萊布尼茨發明二進制之前,已被斯比塞爾稱之為二進制。
有關萊布尼茨二進制與中國古代典籍《
易經 》關係問題的討論涉及如何看待近代中西文化的各自特質以及它們之間的相互作用問題。雖然二進制只是一種算術
記數法 和
計數法 ,但它實際上是特定文化(包括數學、語言、符號、邏輯和哲學等)的產物。現有觀點中的一個明顯不足是把與二進制相關的概念、理論(原理、符號等)的形成與發展看作是單因素的、一次性完成的結果,又把二進制與《易經》哲學和卦圖的相互作用關係看作是“
全或無 ”的關係,從而忽視了概念、理論的形成和變化過程,也容易導致兩種極端的判斷。
因此,立足於近代中西文化交流的大背景,從概念與認知分析入手,能夠把萊布尼茨二進制思想的形成過程置於近代中西文化交流所編織的概念
網路系統 之中,進而梳理出萊布尼茨在秉承西方近代
數學概念 的同時,如何通過獲取和吸納《
易經 》概念資源而實現概念的創造性轉換的脈絡。我們看到,除了萊布尼茨個人的獨創性的偉大貢獻外,近代意義上的二進制實際上是“中西合璧”的產物。