組合數學是一門研究離散對象的科學。
隨著計算機科學的日益發展,組合數學的重要性也日漸凸顯。
組合數學從數千年前開始萌芽,經歷了著名的幻方問題和楊輝三角,直到萊布尼茨正式提出這一科學門類。
基本介紹
- 中文名:組合數學的歷史
- 外文名:Basic Techniques of Combinatorial Theory
概念
起源

阿基米德手稿


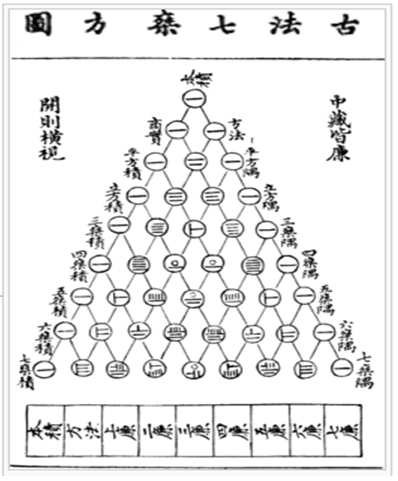
賈憲三角
正式發明


組合數學是一門研究離散對象的科學。
隨著計算機科學的日益發展,組合數學的重要性也日漸凸顯。
組合數學從數千年前開始萌芽,經歷了著名的幻方問題和楊輝三角,直到萊布尼茨正式提出這一科學門類。





組合數學是一門研究離散對象的科學。隨著計算機科學的日益發展,組合數學的重要性也日漸凸顯。組合數學從數千年前開始萌芽,經歷了著名的幻方問題和楊輝三角,直到萊布尼茨...
進入詞條全站搜尋幫助 清除歷史記錄關閉 聲明:百科詞條人人可編輯,詞條創建和...或者從組合學中獨立出來形成數學的一些新分支將是對21世紀數學家們提出的一個新...
數學是中國古代科學中一門重要的學科,它的歷史悠久,成就輝煌。根據它本身發展的特點,可以分為五個時期:①中國古代數學的萌芽;②中國古代數學體系的形成;③中國古代...
當代(1949-)中國科學技術的發展主要從歷史基礎、發展歷程、基礎科學領域的探索與...此外,中國數學家在函式論、馬爾可夫過程、機率套用、運籌學、優選法、組合數學等...
重慶三峽學院數學與統計學院是一所理科學院,歷史悠久,師資雄厚,教職工有48人。...... 比較穩定的研究方向:微分方程與動力系統、代數學、數值分析與智慧型計算、組合數...
數學學院肇始於1923年,是我校歷史悠久的系科之一,首任系主任熊慶來。 [1] ...組合數學、密碼學、糾錯碼理論、數值分析、模糊數學、多元統計分析、運籌學、數學...
《史學經典:中國通史(珍藏版)》完整構架了中國歷史的發展脈絡,全面展示了華夏...組合數學:河圖與洛書 齊魏馬陵之戰 《孫臏兵法》與兵家思想 商鞅誘擒魏公子...
卡塔蘭數是組合數學中一個常在各種計數問題中出現的數列。以比利時的數學家歐仁·查理·卡塔蘭(1814–1894)命名。歷史上,清代數學家明安圖(1692年-1763年)在其《...
