惠特尼不等式

惠特尼不等式 (Whitney's connectivity inequalities) 是圖論中關於圖的連通性的重要不等式，幾乎出現於任何一本圖論教科書中。該不等式明確地指出了圖的點連通性與邊連通性以及與最小度之間的大小關係。但關於該定理的提出者是否是哈斯勒·惠特尼還沒有統一定論。

基本介紹

• 中文名：惠特尼不等式
• 外文名：Whitney’s connectivity inequalities 
  Whitney’s inequalities 
• 別名：惠特尼連通性不等式 
• 表達式：κ(G)≤λ(G)≤δ(G) 
• 提出者：哈斯勒·惠特尼 
• 提出時間：1932年1月 
• 適用領域：組合數學、圖論 
• 所屬學科：數學 、理論計算機科學 

定理介紹

對於一個非平凡圖，滿足

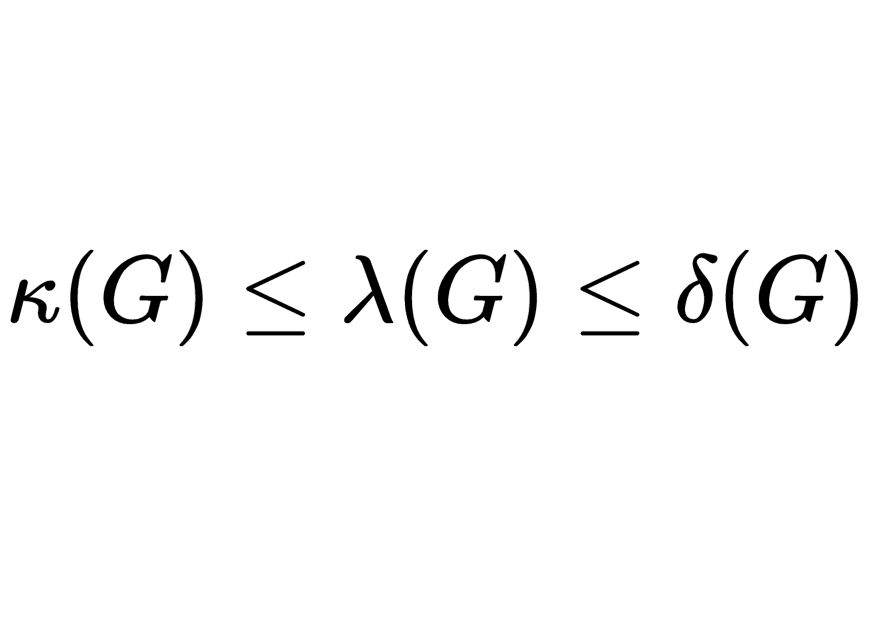
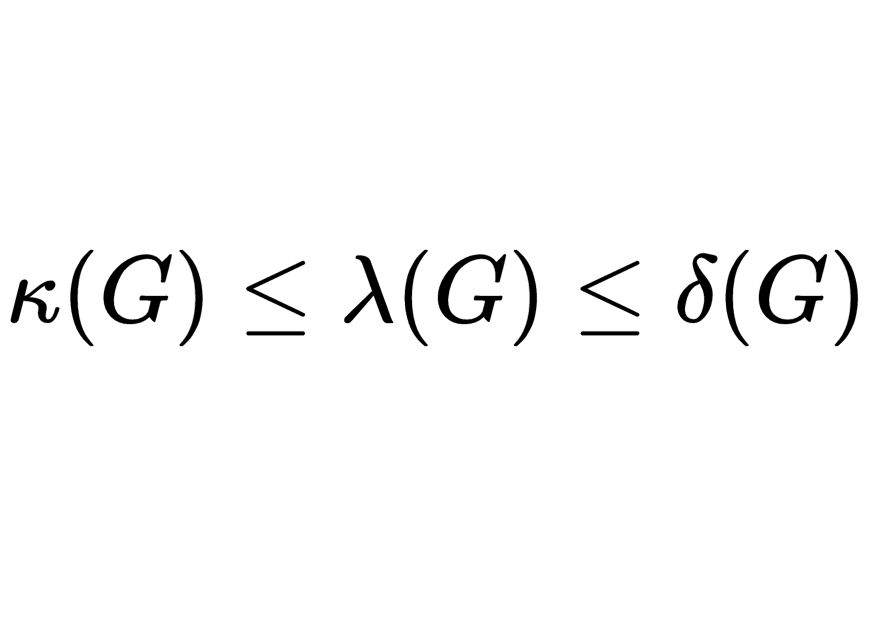
惠特尼不等式表述

其中，表示圖的（點）連通性 (connectivirty)，表示圖的邊連通性 (edge-connectivity)，表示圖的最小度 (minimal degree)。

定理證明

右半邊

由於圖的最小度為，於是考慮中度為的點，。從中刪除與相接的所有邊，則成為孤立點，即與相接的所有邊構成了一個割邊集或稱為不連通邊集 (disconnecting set)，且該不連通邊集的大小。根據邊連通性的定義，。

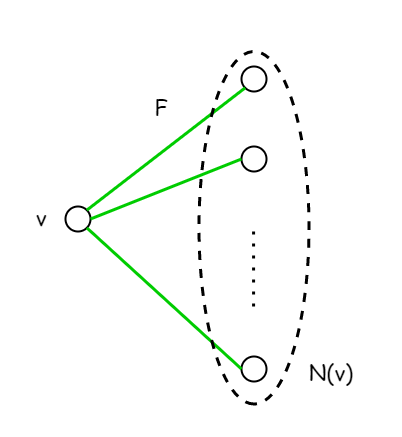
右半不等式的證明

左半邊

考慮圖的最小不連通邊集，只需證明存在圖的一個割集，它們的大小滿足即可。

對於，將圖分割成至少兩個連通分量 (connected component)，這裡取為連通分量，為剩餘部分（不一定為連通分量）。令，顯然中不包含任何邊，否則從中除去該邊，則得到比更小的不連通邊集，與是最小的不連通邊集矛盾。

最小不連通邊集的分割情況

如果，即除去中的點外還有其他點，則可以作為分離與的割集。考慮的大小，斷言。這是因為根據上述分析，中不包含任何邊，而，所以中任意一點均與中至少一條邊相接。於是。

如果，即除去中的點外沒有其他點，此時並不能直接作為割集。任取一點，考慮的鄰居組成的集合。顯然分割了與其他部分，所以可以作為圖的割集，斷言。這是因為，若的鄰居為中的點，則它們之間的邊即為中的邊，所以對於這樣的鄰居，中一個點對應了中一條邊；若的鄰居也是中的點，則一定存在與該鄰居相接的在中的邊，所以對於這樣的鄰居，中一個點對應了中至少一條邊。於是。

連通分量中沒有其他點的情況

相關推論

關於3正則圖的推論

當圖是3正則圖時，。

推論證明

根據惠特尼不等式，已有，只需證明。

考慮圖的最小割集，由於圖是3正則圖，則與餘下被分隔的部分之間的連線只有最多三種類型。對於第一種類型，中的點與連通分量相連1條邊，與剩餘部分相連2條邊，則取與連通分量相連的1條邊加入集合；對於第二種類型，中的點與連通分量相連2條邊，與剩餘部分相連1條邊，則取與剩餘部分相連的1條邊加入集合；對於第三種類型，中的點與連通分量相連1條邊，與剩餘部分相連1條邊，與中的另一點相連一條邊，則取與連通分量相連的1條邊加入集合。顯然，，且是圖的不連通邊集。於是。

3正則圖的割集與不連通邊集

影響意義

一方面，該不等式提供了三個圖的基本量之間的大小關係，為其他不等式以及定理提供了放縮方向；另一方面，該不等式也反映了”高連通性需要圖較為稠密”的組合直觀。