割邊集

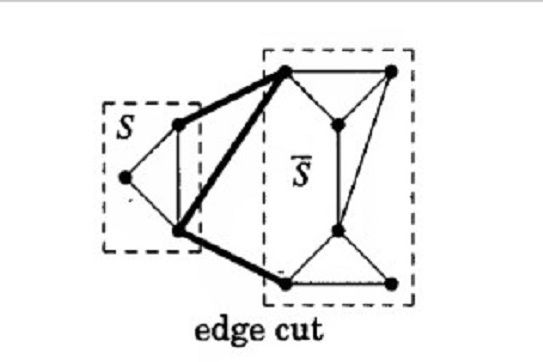
割邊集這一概念，常見於圖論中，是一個邊的集合。在一個連通圖中，通常存在多個割邊集。對於任意一個割邊集，我們在圖中刪去其中的邊，將導致圖的不連通性。割邊集的大小也體現了圖的連通性質，對於刻畫和理解一個圖具有重要意義。

基本介紹

• 中文名：割邊集
• 外文名：edge cut set
• 適用領域：數學，圖論，計算機科學
• 所屬學科：圖論

定義

[S, T]：對於一個圖G=(V, E)，. [S, T]代表一個邊的集合，對於，e的一個端點屬於S，另一個端點屬於T。

割邊集：對於圖G=(V, E)，割邊集是一個形式為的邊的集合，S是V的一個非空子集。注意S和只能通過相連線，所以刪去將會造成S與之間的不連通性。

不連通邊集：連通圖G=(V, E)，不連通邊集，G-F具有多個連通分支。

割邊集與不連通邊集：

每一個割邊集都是一個不連通集，但不連通集不一定是割邊集。割邊集的另一個定義是極小不連通集。

原因：每一個割邊集都會造成圖的不連通性，所以割邊集都是不連通集。但是不連通集不一定能夠表示成割邊集的形式。例如：G=(V, E)，S是V的一個非空子集，，是一個不連通集，但卻不是割邊集。基於T的極小不連通集為是一個割邊集。

bond：極小割邊集。

G=(V, E)是一個連通圖，F是它的一個割邊集，F是一個bond若且唯若G-F恰有兩個連通分支。

證明：

1、G-F有兩個連通分支G1,G2，根據F的定義，F集合中的每一條邊（u, v），。如果F不是一個bond，則必然可以找到一條邊, F-{e'}是一個割邊集。但是由於e'連通G1和G2，G-F+{e'}是一個連通圖，這與割邊集的定義相矛盾。所以F必然是一個bond。

2、如果F是一個bond且G-F有超過兩個連通分支。不妨假設G1,G2,G3是其中的三個連通分支，至少存在滿足.我們令F'=F-e1，在G-F'中，G2, G3依然是兩個分隔開的連通分支，而|F'|＜|F|，所以F’是一個比F更小的割邊集，這與F是一個bond相矛盾。所以G-F只能有兩個連通分支。

邊連通性(edge-connectivity)：F是一個最小的不連通集，我們定義，稱作邊的連通性。由於割邊集是極小不連通集，我們也可以將定義為最小割邊集的大小。

k-edge-connected：G=(V, E)，我們稱G是k-edge-connected若且唯若。

性質

1- 對於連通圖G，.

由於G是一個連通圖，至少刪去一條邊才能造成不連通性，所以。設。我們令邊集F包含所有以v為端點的邊，在G-F中，由於與v相連的邊全部被刪去，所以v是一個孤立點，G-F不是一個連通圖，所以F是一個不連通邊集。根據的定義，.

2- 對於連通圖G，如果存在割邊。

3- S是G中的點集，則有。

證明：

e(G(S))代表屬於S集合中的邊的數量，這些邊的兩個端點均在點集S中。G中的邊共有三類，一種是完全屬於S，一種完全屬於，還有一種是橫跨兩個集合。即代表橫跨兩個集合的邊的數量。在S中使用握手定理可知，對將會給S的度加2，而對於只會給S的度加1.所以我們可知.

4- 對於簡單圖G，S是它的一個非空子集。如果，則可得出。

證明：

根據性質3可知，。

由於，可知，.

再由可得出，,

簡化可得。

套用

割邊集與割點集的關係

1- G=(V,E)，如果G有一條割邊，則G必然有割點，反之則不成立。

證明：

設是一條割邊。則G-(u,v)是一個非連通圖，且u和v分別處於兩個不同的連通分支。。

情況1：，則u為G的一個割點。刪去節點u，相當於同時刪去了邊(u,v)，此時依然有兩個連通分支和。

情況2：，類似於情況1，此時v為G的一個割點，刪去v後得到的連通分支為和。

情況3：，此時G={u,v}。，有割點。

綜合以上三種情況，如果G有一條割邊，則G必然有割點。

2- G=(V,E)，且G中不存在三角形子圖，則。是G中最小的割邊集的大小。

證明：

我們設F為G的最小割邊集，。刪去F將導致G的不連通性，假設此時G分為兩個連通分支。設且C中的點至少與F中的一條邊相連，且。

情況1：，即此時至少有一個點。我們可以令割點集S=C，刪去該割點集，G的兩個連通分支。

情況2：如果，此時中的任意一個節點均與F相連。由於G中不存在三角形子圖，我們可以直到。此時我們可以令割點集S=N(v)，刪去S後，v成為一個孤立點，造成G的不連通性。由於。

3- 如果G是一個3-正則圖，則有。

證明：

設S是G的最小割點集，。設H1,H2是G-S的兩個連通分支。由於S是最小割點集，對於，它必然在H1中有一個鄰居點，在H2中也有一個鄰居點。由於G是一個3-正則圖，，所以它不能同時在H1和H2中有兩個鄰居點。我們假設，則我們刪去邊，即我們只刪去從u到只包含1個鄰居點的邊。

採用這種方法，除了下面討論的情況，我們都可以將H1和H2分隔開。在下面的情況中，v1和v2均在H1和H2中各有一個鄰居點，並且v1與v2相連。如圖2.

我們可以同時刪去v1，v2與H1相連的邊，這樣同樣可以將H1和H2分隔開。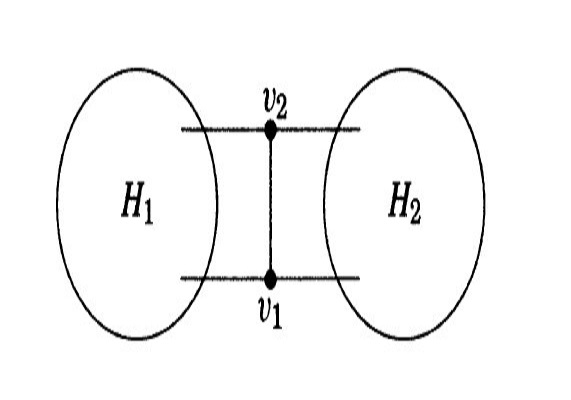

圖 1

綜上，對於割點集中的任何一個點，我們都只需刪去對應的一條邊即可造成不連通性。又已知，所以。

2-edge-connected

我們考察圖G=(V, E)是2-edge-connected的性質：

1-

這是由k-edge-connected的定義所得。

2- 對於G中的任意一條邊，e都在一個圈上。

引理：如果e是一條割邊e不在任意一個圈上。

證明：如果e在一個圈上，且e=(v1,v2)是一條割邊，那么設G1, G2是G-e的兩個連通分支，。由於e=(v1, v2)在一個圈上，刪去e後仍然有一條路徑P連線v1和v2，那么仍有一條路徑P連線G1和G2，所以G1和G2是連通的，這與G1,G2是兩個不同的連通分支相矛盾。

接下來我們採用反證法，假設有一條邊，且e'不在任意一個圈上，根據引理可知，e‘是一條割邊。所以，這與矛盾，所以任意邊e都在一個圈上。

3- G是2-edge-connectedG有一個closed-ear decomposition.

證明：

首先我們分析closed-ear decomposition。

open ear：也簡稱ear, 圖G的一個open ear是一條極大的路徑，它內部點（除去端點）的度是2.如圖

右圖中的P1,P2,P3,P4全是open ear.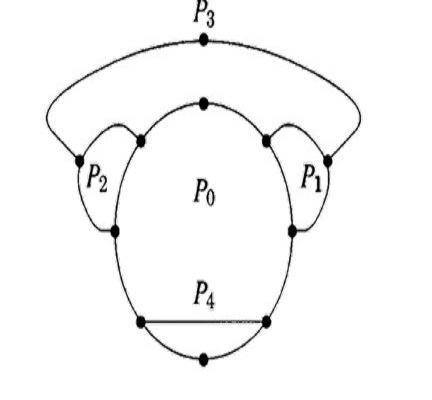

圖 2

closed ear：圖G中的closed ear是一個圈，且closed ear中除了一個點，其他點的度全是2.

如右圖，標記了closed的全是closed ear，而標記了open的則是open ear.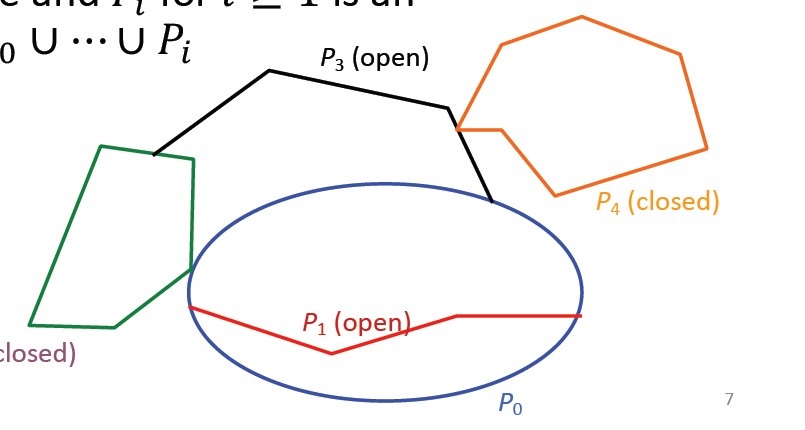

圖 3

closed-ear decomposition: 將G分成P0, P1,..., Pk的組合，且P0是一個圈，其餘的Pi是一個open ear或者closed ear。

必要性：G有一個closed-ear decompositionG是2-edge-connected

我們知道P0是一個圈，對於P0上的任意一條邊，它均在圈P0上。而對於closed ear上的每一條邊，它也在對應的closed ear形成的那個圈上；對於open ear上的邊，由於open ear必然與P0或者其他的ear構成一個圈，所以它們也在一個圈上。這樣，圖G中的每一天邊都在一個圈上，由性質2，G是一個2-edge-connected graph.

充分性：G是2-edge-connectedG有一個closed-ear decomposition

如果G是2-edge-connected，G中至少有一個圈，我們將其命為P0。

G₀=P0，G₁=G₀,..., .

如果，則一定存在邊。由於G是2-edge-connected，e一定落在一個圈上。我們可以找到通過e的圈，它會與相交，根據相交的不同情況：1、如果這個圈經過了中的一條邊，那么我們找到了包含e的一個open ear；2、否則，我們找到一個包含e的open ear。