基本介紹
- 中文名:正則圖
- 外文名:regular graph
- 學科:數學
- 定義:各頂點的度均相同的無向簡單圖
- 性質:每個頂點具有相同數量的鄰點
- 相關名詞:無向簡單圖
簡介,存在性,代數屬性,
簡介
正則圖是指各頂點的度均相同的無向簡單圖。
在圖論中,正則圖中每個頂點具有相同數量的鄰點; 即每個頂點具有相同的度或價態。正則的有向圖也必須滿足更多的條件,即每個頂點的內外自由度都要彼此相等。具有k個自由度的頂點的正則圖被稱為k度的k-正則圖。 此外,奇數程度的正則圖形將包含偶數個頂點。
最多2個等級的正則圖很容易分類:0-正則圖由斷開的頂點組成,1-正則圖由斷開的邊緣組成,2-正則圖由斷開的循環和無限鏈組成,3-正則圖被稱為立方圖。
強規則圖也是常規圖,其中每個相鄰的頂點對具有相同數量的相鄰的相鄰數目,並且每個不相鄰的頂點對具有相同數量的n個相鄰的相鄰公共點。 常規但不太規則的最小圖是循環圖和6個頂點的循環圖。
對於任何Km,完整的圖m是強規則的。
納什 - 威廉士的一個定理說,2k + 1個頂點上的每個k-常規圖都有一個哈密爾頓運算元。
 0-正則圖
0-正則圖 1-正則圖
1-正則圖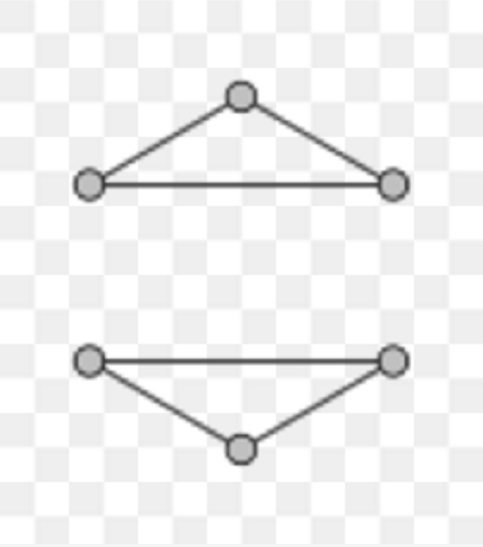 2-正則圖
2-正則圖存在性
眾所周知,k正則圖存在的必要和充分條件是n≥k+1並且nk是偶數。 在這種情況下,通過考慮循環圖的適當參數,可以很容易地構建正則圖。
代數屬性
令A成為正則圖的相鄰矩陣。 然後,若且唯若j={1,1,1,1,1,1}是A的特徵向量時,這個圖才是正則的。 其特徵值將是圖的不變自由度。 對應於其他特徵值的特徵向量與j正交,因此對於這樣的特徵向量v=(v1,v2......vn),我們有,

若且唯若特徵值k具有多重性k時, “唯一的”方向是門階 - 弗羅貝紐斯定理的結果。
還有一個正則和連線圖的標準:若且唯若一個J的矩陣與Jij=1時, 圖的相鄰代數(意思是A的冪的線性組合)。令G為具有直徑D和相鄰矩陣的特徵值的k正則圖

如果G不是二分的話