基本介紹
簡介
歷史
數學表述
























量子電動力學
參見
- 格林恆等式
- 菲涅爾衍射
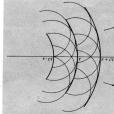
























惠更斯-菲涅耳原理(英語:Huygens–Fresnel principle)是研究波傳播問題的一種分析方法,因荷蘭物理學者克里斯蒂安·惠更斯和法國物理學者奧古斯丁·菲涅耳而命名。這個原理同時適用於遠場極限和近場衍射。惠更斯-菲涅耳原理能夠正確地解釋與...
因此,惠更斯原理是人類對光學現象的一個近似的認識。直到後來,菲涅耳對惠更斯的光學理論作了發展和補充,創立了“惠更斯--菲涅耳原理”,才較好地解釋了衍射現象,完成了光的波動說的全部理論。惠更斯在1678年給巴黎科學院的信和1690年...
他使用了惠更斯-菲涅耳原理去做推導,發現光的波前從障礙物的狹縫中穿出且射到一個距離狹縫有一段距離的螢幕上的效果,跟光的波前直接穿過去是差不多的,看起來就好像沒有經過任何的物理障礙一樣。這個結果表示如果一個縫隙如果非常...
,則衍射波是處於近場,可以使用菲涅耳衍射積分式來計算其物理性質。菲涅耳衍射 假設照射光波於開有孔徑的不透明擋板,則會有衍射圖樣出現於觀察屏。根據惠更斯-菲涅耳原理,從孔徑內部任意點次波源Q發射出的圓球面次波,在觀察屏點P的波...
根據惠更斯-菲涅耳原理,在焦面上的這些衍射圖樣可以看成許多相干次波源,每個次波源的強度正比於該點的振幅。因此在像平面 ∑i上成像過程可以看成從這些次波源發出的光波互相干涉的結果,即所謂成像的兩次衍射過程。要得到一個逼真的像,...
顯然,惠更斯-菲涅耳原理的提出不是為了解決光的自由傳播問題,而是為了求解光通過衍射屏以後的衍射場。為此,取波陣面為包括光孔面∑o、光屏面∑1和無窮遠處的半球面∑2等三部分構成的閉合面。基爾霍夫進一步提出(圖4):∑0面上的...
菲涅耳用波動說成功地解釋了光的衍射現象,他提出的理論方法(現常稱為惠更斯-菲涅耳原理)能正確地計算出衍射圖樣,並能解釋光的直線傳播現象。菲涅耳又進一步解釋了光的雙折射,獲得很大成功。1823年,他根據楊的光波為橫波的學說,和他...
在標量衍射理論中,夫琅禾費近似是對菲涅耳衍射積分的遠場近似式,形式 解釋 夫琅禾費衍射使用惠更斯-菲涅耳原理,藉以把通過圓孔或狹縫的一波動分成多個向外的波動,使用透鏡來有目的地衍射光的觀測實驗一般被用作描述這個原理。當波動...
菲涅耳是從1814年開始研究光學的,他從自己微薄的經濟收入中擠出一部分錢來購買供實驗用的儀器和設備,研究條件十分艱難,但是他勤奮努力,刻苦鑽研,取得了很大成就。他提出了新的惠更斯原理,即惠更斯-菲涅耳原理,完善了光的衍射理論。當...
惠更斯原理的局限 ①沒有說明子波的強度分布問題;②沒有說明波為什麼只能向前傳播,而不向後傳播的問題。後來,菲涅耳對惠更斯原理作了重要的補充,形成惠更斯-菲涅耳原理,這些缺陷才被克服。分類 概述 隨著機械波的傳播,介質中的質點...
菲涅耳用被動說成功地解釋了光的衍射現象,他提出的理論方法(現常稱為惠更斯-菲涅耳原理)能正確地計算出衍射圖樣,並能解釋光的直線傳播現象。菲涅耳又進一步解釋了光的雙折射,獲得很大成功。1823年,他根據楊的光波為橫波的學說,和他...
光的反射定律最初是從實驗得出,根據費馬原理可證明,也可從光的波動觀點出發藉助於惠更斯原理(見惠更斯-菲涅耳原理)從幾何上加以證明,或從電磁場的邊界條件出發從理論上證明。鏡面反射與漫反射 鏡面反射 平行光線經界面反射後沿某一...
這就是菲涅耳區的概念,如圖1所示。原理 在無線信道中,繞射的物理性質取決於障礙物的幾何形狀,繞射點電磁波的振幅、相位和極化狀態。惠更斯-菲涅耳(Huygens—Fresnel)原理清楚地說明了衍射這種現象。如果信道中收發天線之間存在的障礙物占據...
在光學裡,菲涅耳-基爾霍夫衍射公式(Fresnel-Kirchoff's diffraction formula)可以套用於光波傳播的理論分析模型或數值分析模型。[1][2]從菲涅耳-基爾霍夫衍射公式,可以推導出惠更斯-菲涅耳原理,並且解釋一些惠更斯-菲涅耳原理無法解釋的...
十九世紀早期,托馬斯·楊和奧古斯丁·菲涅耳分別做出重大貢獻。托馬斯·楊完成的雙縫實驗顯示出,衍射光波遵守疊加原理,這是牛頓的光微粒說無法預測的一種波動行為。這實驗確切地證實了光的波動性質。奧古斯丁·菲涅耳提出惠更斯-菲涅耳原理,...
1815年,菲涅耳建立了惠更斯-菲涅耳原理,他用此原理計算了各種類型的孔和直邊的衍射圖樣,令人信服地解釋了衍射現象。1818年關於阿拉戈斑(見菲涅耳衍射)的爭論更加強了菲涅耳衍射理論的地位。至此,用光的波動理論解釋光的干涉、衍射和...
1817年,法蘭西學術院舉行了一次關於光的本性問題的科研成果最佳論文競賽,菲涅耳加緊了研究工作;他在他弟弟的幫助下,成功地提出了後人稱之為惠更斯-菲涅耳原理,他用這一原理出色地解釋了光的直線傳播規律,提出了光的衍射理論的子波解釋...
將惠更斯原理加以數學論述,奧古斯丁·菲涅耳證明了光波動說與光在介質內以直線傳播的射線行為相符合,不存在任何矛盾之處。菲涅耳又對於衍射與干涉現象,給出一個合理、完整的解釋。更詳盡細節,請參閱惠更斯-菲涅耳原理。量子物理中對實驗...
楊氏雙縫實驗顯示出,衍射光波遵守疊加原理,這是一種光微粒說無法預測的波行為。這實驗確切地證實了光的波動性質。1818年,奧古斯丁·菲涅耳提出惠更斯-菲涅耳原理,在惠更斯原理的基礎上假定次波與次波之間會彼此發生干涉,又假定次波的...
19世紀初,波動光學初步形成,其中以T. 楊和A.菲涅耳的著作為代表。楊圓滿地解釋了“薄膜的顏色”和雙狹縫干涉現象。菲涅耳於1818年以楊氏干涉原理補充了惠更斯原理,由此形成了今天為人們所熟知的惠更斯-菲涅耳原理,用它可圓滿解釋光的...
