基本介紹
- 中文名：菲涅耳方程
- 外文名：Fresnel equations
- 別名：菲涅耳條件
簡介,簡介,s和p偏振,多重界面的效應,參見,
簡介
簡介
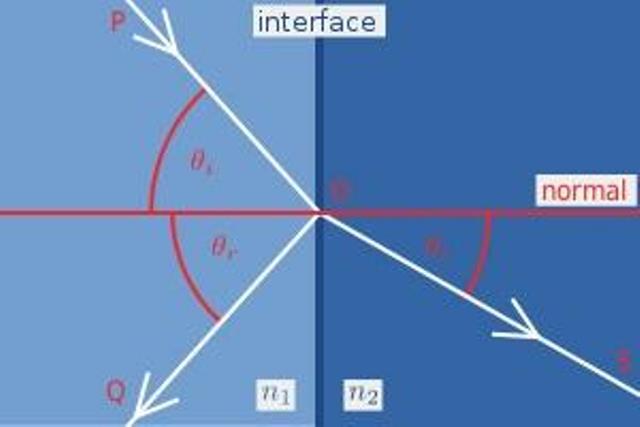
當光從一種具有折射率為
的介質向另一種具有折射率為
的介質傳播時，在兩者的交界處（通常稱作界面）可能會同時發生光的反射和折射。菲涅爾方程描述了不同光波分量被折射和反射的情況。也描述了波反射時的相變。
方程建立在反射面是平面，介質是光滑的，入射光是平面波，邊際效應可被忽略的狀態。
s和p偏振
計算結果取決於入射光的偏振態。以下是兩種情況（由於電場分量、磁場分量、光的傳播方向有右手螺旋關係確定，所以僅討論電場方向的偏振）
- 偏振入射光的電場分量與入射光及反射光所形成的平面相互垂直。此時的入射光狀態稱為“s偏振態”，源於德語“senkrecht”。
- 偏振入射光的電場分量與入射波及反射波所形成的平面相互平行。此時的入射光狀態稱為“p偏振態”，源於德語“parallel”。
多重界面的效應
更多信息：傳遞矩陣方法 (光學)
當光在兩層以上平行表面發生多重反射時，多列反射光波往往會互相發生干涉，從而有可能會使系統總的透射光和反射光振幅表達起來相當複雜，這通常是波長（或頻率）的函式。一個例子是漂浮在水面上的油膜，在光照下會產生多種色彩；其他例子還包括法布里－珀羅干涉儀、透鏡等光學儀器表面所用的能極大降低反射率的鍍膜（增透膜），以及各種光學濾波器。對這些效應的定量計算仍然是基於菲涅耳方程的，但也要考慮額外產生的干涉所帶來的影響，通常可以採用光學中的傳遞矩陣方法來計算這些問題。
參見
- 菲涅耳菱體，菲涅耳用於產生圓偏光的儀器。
- 透射係數
