惠更斯原理是指球形波面上的每一點（面源）都是一個次級球面波的子波源，子波的波速與頻率等於初級波的波速和頻率，此後每一時刻的子波波面的包絡就是該時刻總的波動的波面。其核心思想是：介質中任一處的波動狀態是由各處的波動決定的
基本介紹
- 中文名：惠更斯原理
- 外文名：Huygens principle
- 提出者：克里斯蒂安·惠更斯 Christiaan Huygens
- 提出時間：1690年
- 套用學科：物理
- 適用領域範圍：光學研究
- 適用領域範圍：光學產品開發
- 改進者：菲涅耳 Augustin-Jean Fresnel
簡介,改進,局限性,廣義惠更斯原理,靜電位分布,靜電荷分布,
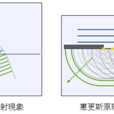
簡介
球形波面上的每一點（面源）都是一個次級球面波的子波源，子波的波速與頻率等於初級
波的波速和頻率，此後每一時刻的子波波面的包絡就是該時刻總的波動的波面。其核心思想是：介質中任一處的波動狀態是由各處的波動決定的。
光的直線傳播、反射、折射等都能以此來進行較好的解釋。此外，惠更斯原理還可解釋晶體的雙折射現象。但是，原始的惠更斯原理是比較粗糙的，用它不能解釋衍射現象，而且由惠更斯原理還會導致有倒退波的存在，而這顯然是不存在的。
由於惠更斯原理的次波假設不涉及波的時空周期特性——波長，振幅和位相，雖然能說明波在障礙物後面拐彎偏離直線傳播的現象，但實際上，光的衍射現象要細微的多，例如還有明暗相間的條紋出現，表明各點的振幅大小不等，對此惠更斯原理就無能為力了。因此必須能夠定量計算光所到達的空間範圍內任何一點的振幅，才能更精確地解釋衍射現象。
改進
菲涅耳在惠更斯原理的基礎上，補充了描述次波的基本特徵——相位和振幅的定量表示式，並增加了“次波相干疊加”的原理，從而發展成為惠更斯—菲涅耳原理。這個原理的內容表述如下：
面積元dS所發出的各次波的振幅和相位滿足下面四個假設：
(1)在波動理論中，波面是一個等相位面。因而可以認為dS面上各點所發出的所有次波都有相同的初位相(可令其為零)。
惠更斯原理 球面
惠更斯原理 球面(3)從面元dS所發次波在P處的振幅正比於dS的面積,且與傾角θ有關，其中θ為dS的法線N與dS到P點的連線r之間的夾角，即從dS發出的次波到達P點時的振幅隨θ的增大而減小(傾斜因數)。
(4)次波在P點處的位相，由光程nr決定。
局限性
惠更斯-菲涅耳原理不是嚴格的理論產物，較大程度上是憑樸素的直覺而得到的，對傾斜因子無法給出具體的函式形式 ，菲涅爾只對它作了某種猜測：θ=0時傾斜因子為1，θ=90時下降到零（即假定無後退次波）。後來古斯塔夫·羅伯特·基爾霍夫（Gustav Robert Kirchhoff）和阿諾德·索末菲（Arnold Johannes Wilhelm Sommerfeld）根據一般的波動理論從理論上導出了與菲涅耳的公式十分接近的衍射公式，同時還給出傾斜因子F（θ）的具體函式形式。
廣義惠更斯原理
靜電位分布
靜電位西分布的廣義惠更斯原理：在靜電場中，一旦離開導體邊界的電位分布，它總有構成圓(或球)的傾向。
眾所周知，靜電位在導體邊界其等位線必須與邊界吻合。然而一離開邊界，它就有圓(或球)的傾向．因為圓(或球)才是真正電位分布的自由態。有時實在因邊界所限，它也儘可能在橢圓(或橢球)之間掙扎，力爭獲得本身的自由。
靜電荷分布
靜電荷Q分布廣義惠更斯原理：在任意導體盤上的面電荷分布有圓的傾向，對於凸圖形盤，它的電心應處於圓心最大展開內切圓的圓心。特別對於三角形盤，此即為內接切圓心。
注意到某些凸圖形相同半徑的內接圓不唯一。這時應取一個幾何上較對稱的內切圓心作為電心。例如平行四邊形，它的內切圓不唯一．我們將取對稱內切圓心O作為電心。
在任意圖形中，以最大展開內切圓心O作為電心，使其可保證在未接觸邊界時有最充分的圓分布可能。這正是電荷分布的本質或自由態，也是廣義惠更斯原理的精華。
