簡要介紹 有限長序列可以通過
離散傅立葉變換 (DFT)將其頻域也離散化成有限長序列。但其計算量太大,很難實時地處理問題,因此引出了快速傅立葉變換(FFT). 1965年,Cooley和Tukey提出了計算
離散傅立葉變換 (DFT)的快速算法,將DFT的運算量減少了幾個數量級。從此,對快速傅立葉變換(FFT)
算法 的研究便不斷深入,
數位訊號處理 這門新興學科也隨FFT的出現和發展而迅速發展。根據對序列分解與選取方法的不同而產生了FFT的多種算法,基本算法是基2DIT和基2DIF。FFT在離散傅立葉反變換、線性
卷積和 線性相關 等方面也有重要套用。
快速傅立葉變換 快速傅氏變換(FFT),是
離散 傅氏變換的快速
算法 ,它是根據離散傅氏變換的奇、偶、虛、實等特性,對離散
傅立葉變換 的算法進行改進獲得的。它對傅氏變換的理論並沒有新的發現,但是對於在計算機系統或者說
數字系統 中套用離散
傅立葉變換 ,可以說是進了一大步。
設x(n)為N項的複數序列,由DFT變換,任一X(m)的計算都需要N次複數乘法和N-1次複數加法,而一次複數乘法等於四次實數乘法和兩次實數加法,一次複數加法等於兩次實數加法,即使把一次複數乘法和一次複數加法定義成一次“運算”(四次實數乘法和四次實數加法),那么求出N項複數序列的X(m),即N點DFT變換大約就需要N^2次運算。當N=1024點甚至更多的時候,需要N2=1048576次運算,在FFT中,利用WN的周期性和對稱性,把一個N項序列(設N=2k,k為正整數),分為兩個N/2項的子序列,每個N/2點DFT變換需要(N/2)^2次運算,再用N次運算把兩個N/2點的DFT變換組合成一個N點的DFT變換。這樣變換以後,總的運算次數就變成N+2*(N/2)^2=N+N^2/2。繼續上面的例子,N=1024時,總的運算次數就變成了525312次,節省了大約50%的運算量。而如果我們將這種“一分為二”的思想不斷進行下去,直到分成兩兩一組的DFT運算單元,那么N點的DFT變換就只需要Nlog2N次的運算,N在1024點時,運算量僅有10240次,是先前的直接算法的1%,點數越多,運算量的節約就越大,這就是FFT的優越性。
快速傅立葉變換 快速傅立葉變換 基本思想 FFT的基本思想是把原始的N點序列,依次分解成一系列的短序列。充分利用DFT計算式中指數因子 所具有的對稱性質和周期性質,進而求出這些短序列相應的DFT並進行適當組合,達到刪除重複計算,減少乘法運算和簡化結構的目的。此後,在這思想基礎上又開發了高基和分裂基等快速算法,隨著數位技術的高速發展,1976年出現建立在數論和多項式理論基礎上的維諾格勒傅立葉變換算法(WFTA)和素因子傅立葉變換算法。它們的共同特點是,當N是素數時,可以將DFT算轉化為求循環卷積,從而更進一步減少乘法次數,提高速度。
算法類型 FFT算法很多,根據實現運算過程是否有指數因子WN 可分為有、無指數因子的兩類算法。
有指數因子的算法
經典庫利-圖基算法 當輸入序列的長度N不是素數(素數只能被1而它本身整除)而是可以高度分解的複合數,即N=N1 N2 N3 …Nr時,若N1 =N2 =…=Nr =2,N=2則N點DFT的計算可分解為N=2×N/2,即兩個N/2點DFT計算的組合,而N/2點DFT的計算又可分解為N/2=2×N/4,即兩個N/4點DFT計算的組合。依此類推,使DFT的計算形成有規則的模式,故稱之為以2為基底的FFT算法。同理,當N=4時,則稱之為以4為基底的FFT算法。當N=N1·N2 時,稱為以N1 和N2 為基底的混合基算法。
在這些算法中,基2算法用得最普遍。通常按序列在時域或在頻域分解過程的不同,又可分為兩種:一種是時間抽取FFT算法(DIT),將N點DFT輸入序列x(n)、在時域分解成2個N/2點序列而x1 (n)和x2 (n)。前者是從原序列中按偶數序號抽取而成,而後者則按奇數序號抽取而成。DIT就是這樣有規律地按奇、偶次序逐次進行分解所構成的一種快速算法。
分裂基算法(RSFFT) 1984年由P.杜哈美爾和H.赫爾曼等導出的一種比庫利圖基算法更加有效的改進算法,其基本思想是在變換式的偶部採用基2算法,在變換式的奇部採用基4算法。優點是具有相對簡單的結構,非常適用於實對稱數據,對長度N=2能獲得最少的運算量(乘法和加法),所以是選用固定基算法中的一種最佳折衷算法。
計算方法 計算
離散傅立葉變換 的快速方法,有按時間抽取的FFT算法和按
頻率 抽取的FFT算法。前者是將時域
信號序列 按偶奇分排,後者是將頻域信號序列按偶奇分排。它們都藉助於的兩個特點:一是周期性;二是對稱性,這裡符號*代表其共軛。這樣,便可以把
離散傅立葉變換 的計算分成若干步進行,計算效率大為提高。
時間抽取 算法 令
信號序列 的長度為
N =2,其中
M 是正整數,可以將時域信號序列
x (
n )分解成兩部分,一是偶數部分
x (2
n ),另一是
奇數 部分
x (2
n +1),於是信號序列
x (
n )的
離散傅立葉變換 可以用兩個
N /2抽樣點的離散傅立葉變換來表示和計算。考慮到和
離散傅立葉變換 的周期性,式⑴可以寫成
⑶其中(4a)(4b)由此可見,式⑷是兩個只含有
N /2個點的
離散傅立葉變換 ,
G (
k )僅包括原信號序列中的偶數點序列,
H (
k )則僅包括它的奇數點序列。雖然
k =0,1,2,…,
N -1,但是
G (
k )和
H (
k )的周期都是
N /2,它們的數值以
N /2周期重複。
因為於是由式⑶和式⑷得到(5a)(5b)
因此,一個抽樣點數為
N 的信號序列
x (
n )的
離散傅立葉變換 ,可以由兩個
N /2抽樣點序列的離散傅立葉變換求出。依此類推,這種按時間抽取算法是將輸入信號序列分成越來越小的子序列進行
離散傅立葉變換 計算,最後合成為N點的離散傅立葉變換。
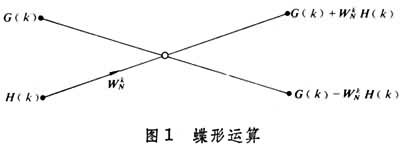
通常用圖1中蝶形算法的信號流圖來表示式⑸的
離散傅立葉變換 運算。例如,
N =8=2的抽樣點的信號序列
x (
n )的
離散傅立葉變換 ,可用如圖2所示的FET算法的信號流圖來計算。
①
N =2點的
離散傅立葉變換 的計算全由
蝶形運算 組成,需要
M 級運算,每級包括
N /2個蝶形運算,總共有 個蝶形運算。所以,總的計算量為次複數
乘法 運算和
N log2
N 次複數加法運算。
⑹N 抽樣點的輸入信號具有N 個原始數據x 0(n ),經第一級運算後,得出新的N 個數據x 1(n ),再經過第二級疊代運算,又得到另外N 個數據x 2(n ),依此類推,直至最後的結果x (k )=xM (k )=X (k )在逐級疊代計算中,每個蝶形運算的輸出數據存放在原來存貯輸入數據的單元中,實行所謂“即位計算”,這樣可以節省大量存放中間數據的暫存器。
③
蝶形運算 中
加權 係數隨疊代級數成倍增加。由圖2可以看出係數的變化規律。對於
N =8,
M =3情況,需進行三級疊代運算。在第一級疊代中,只用到一種
加權 係數;
蝶形運算 的跨度間隔等於1。在第二級疊代中,用到兩種加權係數即、;
蝶形運算 的跨度間隔等於2。在第三級疊代中,用到4種不同的加權係數即、、、;
蝶形運算 的跨度間隔等於4。可見,每級疊代的不同加權係數的數目比前一級疊代增加一倍;跨度間隔也增大一倍。
④ 輸入數據序列x (n )需重新排列為x (0)、x ⑷、x ⑵、x ⑹、x ⑴、x ⑸、x ⑶、x ⑺,這是按照二進制數的碼位倒置所得到的反序數,例如N =8中數“1”的二進制數為“001”,將其碼位倒轉變為“100”,即為十進制數“4”。
頻率抽取算法 按頻率抽取的 FFT算法是將頻域信號序列
X (
k )分解為奇偶兩部分,但算法仍是由時域信號序列開始逐級運算,同樣是把
N 點分成
N /2點計算FFT,可以把直接計算
離散傅立葉變換 所需的
N 次乘法縮減到次。
在N =2的情況下,把N 點輸入序列x (n )分成前後兩半
⑺
時間序列
x 1(
n )±
x 2(
n )的長度為
N /2,於是
N 點的
離散傅立葉變換 可以寫成
(8a)
(8b)
頻率信號序列
X (2l)是時間信號序列
x 1(
n )+
x 2(
n )的
N /2點
離散傅立葉變換 ,頻率信號序列
X (2l+1)是時間信號序列【
x 1(
n )-
x 2(
n )】的
N /2點離散傅立葉變換,因此,
N 點離散傅立葉變換的計算,通過兩次加(減)法和一次乘法,從原來序列獲得兩個子序列,所以,頻率抽取算法也具有蝶形運算形式。以2為基數的FFT基本
蝶形運算 公式為
⑼
其計算量完全和時間抽取算法一樣,即只需次乘法運算和
N log2
N 次加(減)法運算。圖3 表示
N =8=2點的
離散傅立葉變換 的信號流圖。由圖可見,它以三級疊代進行即位計算,輸入數據是按自然次序存放,使用的係數也是按自然次序,而最後結果則以二進制反序存放。
實際上,頻率抽取
算法 與時間抽取算法的信號流圖之間存在著
轉置 關係,如將流圖適當變形,可以得出多種幾何形狀。
除了基2的FFT
算法 之外,還有基4、基8等高基數的FFT算法以及任意數為基數的FFT算法。
套用 計算量小的顯著的優點,使得FFT在信號處理技術領域獲得了廣泛套用,結合高速硬體就能實現對信號的實時處理。例如,對語音信號的分析和合成,對通信系統中實現全數位化的時分制與頻分制(TDM/FDM)的復用轉換,在頻域對信號濾波以及相關分析,通過對雷達、聲納、振動信號的頻譜分析以提高對目標的搜尋和跟蹤的解析度等等,都要用到FFT。可以說FFT的出現,對數位訊號處理學科的發展起了重要的作用。
參考書目 何振亞著:《
數位訊號處理 的理論與套用》下冊,人民郵電出版社,北京,1983。
程乾生著:《
數位訊號處理 》,北京大學出版社,北京,2003。
E.O.布里漢著,柳群譯:《快速傅立葉變換》,上海科學技術出版社,1979。(E. O. Brigham,The Fast Fourier Transform ,Prentice Hall,Englewood Cliffs,New Jersey,1974.)v

 快速傅立葉變換
快速傅立葉變換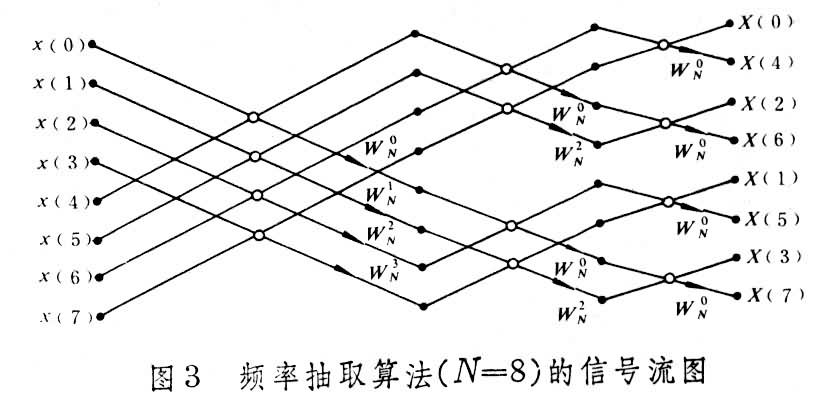 快速傅立葉變換
快速傅立葉變換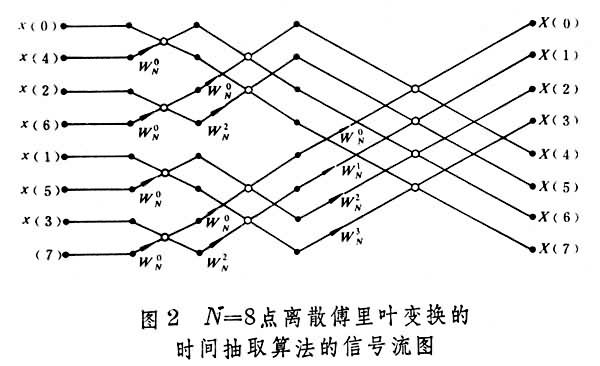 快速傅立葉變換
快速傅立葉變換

 快速傅立葉變換
快速傅立葉變換 快速傅立葉變換
快速傅立葉變換 快速傅立葉變換
快速傅立葉變換