基本介紹
- 中文名:循環不變數
- 外文名:loop invariant
- 性質:不變數
- 領域:計算機
概述
霍爾邏輯
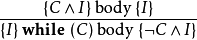
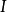
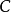

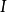
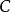
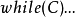
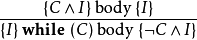
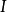
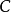

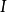
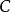
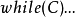
循環不變數(loop invariant)是一個不變數,被用來證明循環的特點,更多地,算法使用循環 (usually 正確性)。非正式的說,一個循環不變數是指在循環開始和循環中每...
如果數組邊界檢查位在循環體中,循環邊界和數組長度都是循環不變數,並且數組索引變數是循環歸納變數,那么可以通過把邊界檢查移出循環體來減少數組邊界檢查的執行次數。...
2.12 循環不變數:將十進制數轉換為二進制數2.13 常見的錯誤2.14 小結第3章 算法分析3.1 引言3.2 符號O3.3 時間與空間複雜度3.4 習之和...
13.5 循環改進 i 75513.5.1 循環不變數 75513.5.2 歸納變數 75613.6 指令調度 75913.7 循環改進 ii 76313.7.1 循環展開和軟體流水線 763...
9. 5. 6 循環不變數 2179. 5. 7 SPARK 工具 220習題221第十章 軟體故障消除 22410. 1 為什麼要故障消除 22410. 2 審查 225...
2.4 設計正確的算法和程式252.4.1 斷言和不變數262.4.2 循環不變數262.4.3 數據結構不變數272.4.4 驗證算法272.5 一個示例: 二分查找272.6 基本算法分析29...
7.2.13 for循環 7.2.14 函式調用 7.3 聲明 7.3.1 變數定義 7.3.2 函式定義 7.3.3 片段 程式設計:翻譯成樹 習題 第8章 基本塊和軌跡 8.1 規範...
2.4.1斷言和不變數26 2.4.2循環不變數26 2.4.3數據結構不變數27 2.4.4驗證算法27 2.5一個示例:二分查找27 2.6基本算法分析29 2.6.1求和29 2...
4.5.5循環不變數 練習 關鍵術語和結果 複習題 補充練習 計算機題目 計算和研究 寫作題目 第5章計數 5.1計數的基礎 5.1.1引言 5.1.2基本的計數原則 5.1....
3.1.1 消除循環不變數 3.1.2 減少過程調用 3.1.3 消除不必要的記憶體存取 3.2 阻礙最佳化的因素 3.2.1 編譯最佳化選項 3.2.2 變數別名 3.2.3 函式調用的邊際...
6.3 程式控制循環 215 6.3.1 循環不變數 216 6.3.2 函式調用 217 6.3.3 數組引用 219 6.3.4 分解複合布爾表達式 220 6.3.5 循環展開 221 6.3.6 循環干涉...
多數編譯器都可基於數據流分析實現別名分析、常數拆疊、常數傳播、公共子表達式消除、冗餘代碼和死碼刪除、循環不變數的移動、循環逆轉、循環展開、函式嵌入等與體系...
7.2.12 while循環7.2.13 for循環7.2.14函式調用7.3聲明7.3.1變數定義7.3.2函式定義程式設計:翻譯成樹習題第8章 基本塊和軌跡8.1規範樹...
