基本介紹
- 中文名：復球面
- 外文名：Complex Sphere
- 領域：空間幾何
- 特殊點：北極N，南極O
- 相關概念：擴充複平面
- 類型：空間幾何領域術語
定義,擴充複平面上的幾個概念,
定義
複數還有一種幾何表示法，它是借用地圖製圖學中將地球投影到平面上的測地投影法，建立複平面與球面上的點的對應，著重說明引入無窮遠點的合理性。
取一個在原點O與z平面相切的球面，通過O點作一垂直於z平面的直線與球面交於N點，稱為北極，O稱為南極，如圖1所示。用直線段將N與z平面上一點z相連，此線段交球面於一點P(z)，這樣就建立起球面上的點(不包括北極點N)與複平面上的點間的一一對應。
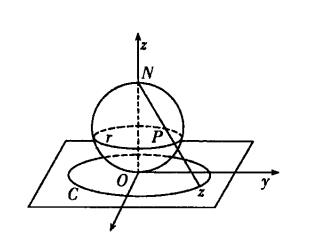
圖1 負面球
考慮z平面上一個以原點為中心的圓周C，在球面上對應的也是一個圓周
(即是緯線)，當圓周C的半徑越大時，圓周就越趨於北極N。因此北極N可以看成是與z平面上的一個模為無窮大的假想點相對應，這個假想點稱為無窮遠點(infinite—point)，並記為
．複平面加上點後稱為擴充複平面(extended complex plane)，與它對應的就是整個球面，稱為復球面(complexsphere)．簡單說來，擴充複平面的一個幾何模型就是復球面。
關於新“數”還需作如下幾點規定：
(1)運算
無意義；
(2)
時，
；
(3)
(但可為)時，
；
(4)的實部、虛部及幅角都無意義；
(5)複平面上每一條直線都通過點．
擴充複平面上的幾個概念
(1)在擴充複平面上，無窮遠點的鄰域應理解為以原點為心的某圓周的外部，即的
鄰域
，是指適合於條件
的點集．對比開集及邊界的定義，在擴充複平面上，內點和邊界點等概念均可以推廣到點．於是，複平面以為其唯一的邊界點；擴充複平面以為內點，且它是唯一的無邊界的區域．
(2)單連通的概念也可推廣到擴充複平面上的區域上．對擴充複平面上的區域D，關於單連通的概念可不加更改地移到這裡來。但要注意，D內的簡單閉曲線在D內連續收縮於一點，這個點既可能是有限點，也可能是點；而所謂r能連續收縮到點，實際上就是，逐漸擴大而最後落入點的任意小的鄰域中，亦即落入以原點為中心，任意大為半徑的圓周外部。
初看起來，這種收縮於點的說法好像很不自然，它與收縮於一有限點似乎極不相似，但如果放在復球面上來考慮，問題就很清楚了；所謂在擴充複平面上，收縮於一點
，也就是它在復球面上的對應曲線收縮於在復球面上的對應點
；也可能是北極點(對應於
)，也可能不是北極點(對應於
)。這樣就可立刻看出，這兩種情況算沒有本質的區別。
注意，在擴充複平面上，一個圓周的外部(這裡把算作這個區域的內點)就是一個單連通區域。所以，一個無界區域，考慮它是否單連通，首先要考慮是在通常的複平面上還是在擴充複平面上講的(當在擴充複平面上時，還要問是否算在這個區域內)。
如在無界區域的邊界上，也就是區域的邊界曲線延伸到，則不論在通常複平面上，還是在擴充複平面上，區域是否為單連通必定是一致的。
