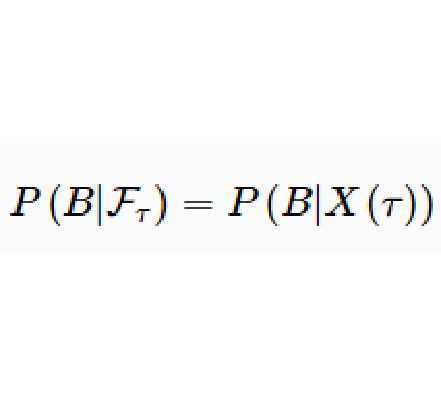強馬爾可夫過程

強馬爾可夫過程(strong Markov process)，指這樣一種隨機過程，在已知它狀態條件下，它未來的演變(將來)不依賴於它以往的演變(過去)。這種已知“現在”的條件下，“將來”與“過去”無關的特性稱為馬爾可夫性。其中，“現在”是指固定時刻。但實際問題中常需將馬爾可夫性中的“現在”這個時刻概念推廣為停時。直觀上講，停時是描述某種隨機現象發生的時刻，它是普通時間變數的隨機化。例如，考察從圓心出發的平面上的布朗運動，要研究首次到達圓周的時刻t以前的事件和以後的事件的條件獨立性，這裡的t就是停時，並認為t是“現在”。這種把“現在”推廣為停時情形的“現在”，且在已知“現在”的條件下，“將來”與“過去”無關的特性被稱為強馬爾可夫性。具有此性質的馬爾可夫過程稱為強馬爾可夫過程。以前，許多人認為馬爾可夫過程必然是強馬爾可夫過程。直到1956年，才有人找到馬爾可夫過程不是強馬爾可夫過程的例子。馬爾可夫過程理論的進一步發展表明，強馬爾可夫過程才是馬爾可夫過程的真正研究對象。

基本介紹

• 中文名：強馬爾可夫過程
• 外文名：strong Markov process
• 屬性：一類隨機過程
• 性質：強馬爾可夫性
• 相關概念：馬爾可夫性、馬爾可夫過程等

定義

強馬爾可夫過程(strong Markov process)是一類隨機過程，指具有比馬爾可夫性更強的條件無後效性的隨機過程。如果對於任意停時和(後代數)，有

其中是前代數，則稱馬爾可夫過程是強馬爾可夫過程。由等式(1)刻畫的性質稱為強馬爾可夫性。因為任意非負常數都是一個停時，所以(1)式是“馬爾可夫過程”中性質2的加強(參見下文“馬爾可夫過程”)，而強馬爾可夫性只不過是在描述馬爾可夫性的等式中用任意停時代替任意固定的時刻。

許多常見的馬爾可夫過程，例如，離散時間參數馬爾可夫過程，布朗運動等都具有強馬爾可夫性，但也存在馬爾可夫過程不是強馬爾可夫過程的例子。

馬爾可夫過程

馬爾可夫過程(Markov process)簡稱馬氏過程，是一類重要的隨機過程。設為定義在機率空間上取值於可測空間的隨機過程，為的上升域族，.如果下面的性質1成立：

1.

則稱過程為馬爾可夫過程，可測空間稱為馬爾可夫過程的狀態空間。一般情形下，因為要考慮形如集合的機率，人們還要求E包含所有單點集性質1與下列性質之一等價：

2.

3.

注意，若性質1，2，3成立，則把其中的換成的自然域族後相應的性質仍成立，而且這時性質2有如下的直觀意義：當已知系統在時刻以前(含)的歷史時，系統在以後的發展只依賴於系統在時刻的狀態而與它在以前的情況無關，此即所謂馬爾可夫性，這正是馬爾可夫過程的本質所在。

應當指出，儘管一些著作中也把馬爾可夫性稱為無後效性，但它和多數著作中提到的無後效性是不一樣的，後者是指過程的獨立增量性質。相對於此，馬爾可夫性只是一種條件無後效性。