康托爾函式

在數學中，以數學家格奧爾格·康托爾命名的康托爾函式，是一個一致連續，卻不絕對連續的函式。

基本介紹

• 中文名：康托爾函式
• 屬性：數學套用
• 特點：對於有限集合是明顯的

定義

康托爾函式 c: [0,1] → [0,1] ，對於x∈[0,1]，其函式值c(x)可由以下步驟得到：

1. 以三進制表示x。
   
2. 如果x中有數字1，就將第一個1之後的所有數字換成0。
   
3. 將所有數字2換成數字1。
   
4. 以二進制讀取轉換之後的數，這個數即為c(x)。
   

例如：

• 1/4以三進制表示為0.020202...，其中並沒有1，因此經過第二步仍然是0.020202...，第三步轉換為0.010101...，將其視為二進制，則為1/3，因此c(1/4)=1/3。
  
• 1/5以三進制表示為0.01210121...，第二步轉換為0.01，由於其中沒有2，因此經過第三步後仍是0.01，視為二進制則為1/4，因此c(1/5)=1/4。
  
• 200/243以三進制表示為0.21102(即0.2110122222...)，第二步轉換為0.21，第三步轉換為0.11，視為二進制則為3/4，因此c(200/243)=3/4。
  

其它定義

性質構造

若在[0, 1]上定義的f(x)滿足下列四個條件，則f(x)即為康托爾函式

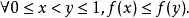
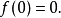
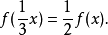
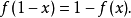
疊代構造

下面我們構造一個函式序列{f_n(x)}，這個序列將收斂於康托爾函式： 首先定義

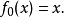
接下來，對於每個正整數n，函式f_n+1(x)都由函式f_n(x)定義：

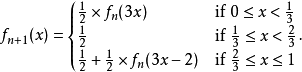
檢查 f_n(x)是否每個點都收斂於之前定義的康托爾函式，我們可以發現，

設f(x)是極限函式, 那么對於任意非負整數n都有，

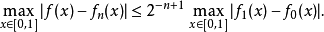
另外可以注意到只要滿足f₀(0)= 0, f₀(1)= 1 且f₀有界，起始函式f₀(x)具體是什麼函式並不重要。