熵是刻畫巴拿赫空間中緊集“大小”或“粗細”的不變數之一,在函式逼近論中的套用研究開始於20世紀50年代,以後逐漸得到發展。區別於機率論中的同名概念,稱為集A的度量熵。
基本介紹
- 中文名:度量熵
- 外文名:metric entropy
- 適用範圍:數理科學
簡介
ε覆蓋
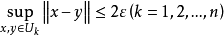
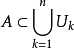
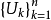
定義
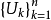
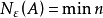
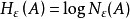
另一提法
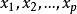
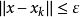
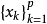
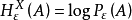
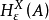

熵是刻畫巴拿赫空間中緊集“大小”或“粗細”的不變數之一,在函式逼近論中的套用研究開始於20世紀50年代,以後逐漸得到發展。區別於機率論中的同名概念,稱為集A的度量熵。
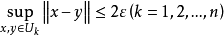
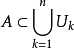
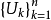
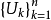
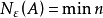
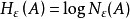
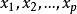
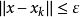
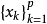
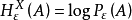
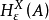

熵是刻畫巴拿赫空間中緊集“大小”或“粗細”的不變數之一,在函式逼近論中的套用研究開始於20世紀50年代,以後逐漸得到發展。區別於機率論中的同名概念,稱為集A的...
直到1948年,香農提出了“信息熵”的概念,才解決了對信息的量化度量問題。信息熵這個詞是C.E.香農從熱力學中借用過來的。熱力學中的熱熵是表示分子狀態混亂程度的...
凝聚態的熵在等溫過程中的改變隨絕對溫度趨於0。通過可逆的、微小的、遲緩的變化,物質進入另一種不同的狀態,其中自然包括分裂為兩個或多個物理、化學性質不同的...
相對熵(relative entropy),又被稱為Kullback-Leibler散度(Kullback-Leibler divergence)或信息散度(information divergence),是兩個機率分布(probability distribution)間...
熵定律是科學定律之最,這是愛因斯坦的觀點。我們知道能源與材料、信息一樣,是物質世界的三個基本要素之一,而在物理定律中,能量守恆定律是最重要的定律,它表明了...
熵,熱力學中表征物質狀態的參量之一,用符號S表示,其物理意義是體系混亂程度的度量。...
在資訊理論中,熵是對不確定性的一種度量。信息量越大,不確定性就越小,熵也就越小;信息量越小,不確定性越大,熵也越大。根據熵的特性,我們可以通過計算熵值來...
熵的概念是由德國物理學家克勞修斯於1865年所提出。最初是用來描述“能量退化”的物質狀態參數之一,在熱力學中有廣泛的套用。但那時熵僅僅是一個可以通過熱量改變...
利用絕熱過程中的熵是不變還是增加來判斷過程是可逆還是不可逆的基本原理。利用克勞修斯等式與不等式及熵的定義可知,在任一微小變化過程中恆有熵增加原理,其中不等...
1948 年,香農提出了“信息熵”(shāng) 的概念,解決了對信息的量化度量問題。一條信息的信息量大小和它的不確定性有直接的關係。比如說,我們要搞清楚一件非常...
譜熵(spectral entropy )這一概念描述了功率譜和熵率之間的關係。研究表明,由自回歸模型估計出的譜具有最大的譜熵,因而是一種理想的求譜方法,稱為最大熵譜估計...
圖像熵(image entropy)是圖像“繁忙”程度的估計值。...... 圖像熵(image entropy)是圖像“繁忙”程度的估計值...其中,K是與選擇的度量單位相對應的一個正比常數...
信息熵是信息無序度的度量,信息熵越大,信息的無序度越高,其信息的效用值越小;反之,信息的熵越小,信息的無序度越小,信息的效用值越大。在綜合評價中,可以...
物理定義:熵增過程是一個自發的由有序向無序發展的過程(Bortz, 1986; Roth, 1993)。 熱力學定義:熵增加,系統的總能量不變,但其中可用部分減少。統計學定義:熵...
熵值法 1、基本原理 在資訊理論中,熵是對不確定性的一種度量。信息量越大,不確定性就越小,熵也就越小;信息量越小,不確定性越大,熵也越大。根據熵的特性,...
最大熵法是利用已知的自相關函式值來外推未知的自相關函式值,去除了對未知數據的人為假定,從而使譜估計的結果更為合理。熵在資訊理論中是信息的度量,事件越不確定...
熵的概念是由資訊理論的創始人申農(Shannon)提出的,在統計學中用它作為隨機事件不確定程度的一種度量,描述給定長度為n的隨機變數序列的熵隨n的增長情況。...
地球信息熵(Ceographic Infomation Entropy)是指地球信息載體的信息量。地球信息熵是指信息載體中的信息與噪聲(Noise)之比,簡稱“信噪比”。C.E.Shannon以搞作為...
最大熵譜估計(maximum entropy spectral estimation)信號功率譜密度估計的一種方法。1967年,由J.P.伯格提出。...
最大熵原理是一種選擇隨機變數統計特性最符合客觀情況的準則,也稱為最大信息原理。隨機量的機率分布是很難測定的,一般只能測得其各種均值(如數學期望、方差等)或...
第六章 企業組織管理系統協同複雜性度量第一節 企業系統的組織協同性複雜性分析第二節 企業系統組織協同複雜性的評價模型建立第三節 企業系統的協同複雜性度量熵...
