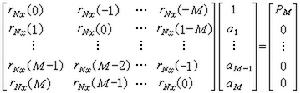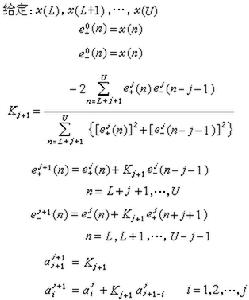對信號的功率譜密度估計的一種方法。1967年由J.P.伯格所提出。其原理是取一組時間序列，使其自相關函式與一組已知數據的自相關函式相同，同時使已知自相關函式以外的部分的隨機性最強，以所取時間序列的譜作為已知數據的譜估值。
基本介紹
- 中文名：最大熵法
- 外文名： maximum entropy method (MEM)
- 類別：科學
- 內容：信號功率譜密度估計
- 發明人：J.P.伯格
正文,
正文
對信號的功率譜密度估計的一種方法。1967年由J.P.伯格所提出。其原理是取一組時間序列，使其自相關函式與一組已知數據的自相關函式相同，同時使已知自相關函式以外的部分的隨機性最強，以所取時間序列的譜作為已知數據的譜估值。它等效於根據使隨機過程的熵為最大的原則,利用N個已知的自相關函式值來外推其他未知的自相關函式值所得到的功率譜。最大熵法功率譜估值是一種可獲得高解析度的非線性譜估值方法，特別適用於數據長度較短的情況。
最大熵法譜估值對未知數據的假定 一個平穩的隨機序列，可以用周期圖法對其功率譜進行估值。這種估值方法隱含著假定未知數據是已知數據的周期性重複。現有的線性譜估計方法是假定未知數據的自相關函式值為零，這種人為假定帶來的誤差較大。最大熵法是利用已知的自相關函式值來外推未知的自相關函式值，去除了對未知數據的人為假定，從而使譜估計的結果更為合理。
熵在資訊理論中是信息的度量，事件越不確定，其信息量越大，熵也越大。對於上述問題來說，對隨機過程的未知的自相關函式值，除了從已知的自相關函式值得到有關它的信息以外，沒有其他的先驗知識。因而，在外推時，不希望加以其他任何新的限制，亦即使之“最不確定”。換言之，就是使隨機過程的熵最大。
最大熵法功率譜估值表達式
最大熵法功率譜估值表達式
最大熵法功率譜估值的表達式為式中PM為M階預測誤差濾波器的輸出功率;B為隨機過程的頻寬;Δt=1/2B為採樣周期;ɑm(m=1,2,…,M)由下式決定：
其中rNx(M)為已知的隨機過程的自相關函式值。
從功率譜估值的表達式可以看出，最大熵法與自回歸信號模型分析法以及線性預測誤差濾波器是等價的，只是從不同的觀點出發得到了相同的結果。
由已知信號計算功率譜估值的遞推算法 套用上述的譜估值表達式進行計算時，需要知道有限個自相關函式值。但是，實際的情況往往是只知道有限長的時間信號序列，而不知道其自相關函式值。為了解決這個問題，J.P.伯格提出了一種直接由已知的時間信號序列計算功率譜估值的遞推算法，使最大熵法得到廣泛的套用。遞推算法如下：
由已知信號計算功率譜估值的遞推算法 套用上述的譜估值表達式進行計算時，需要知道有限個自相關函式值。但是，實際的情況往往是只知道有限長的時間信號序列，而不知道其自相關函式值。為了解決這個問題，J.P.伯格提出了一種直接由已知的時間信號序列計算功率譜估值的遞推算法，使最大熵法得到廣泛的套用。遞推算法如下：
遞推算法只需要知道有限長的時間信號序列，不須計算其自相關函式值,所得的解保證是穩定的。但是,其解只是次優解。
套用遞推算法往往使譜估值出現“譜線分裂“與“頻率偏移”等問題，因而,又有各種改進的算法。其中,較著名的有傅格算法和馬普爾算法，但是所需的計算量較大。另外，在有噪聲的情況下，如何選定階數仍有待進一步探討。
套用遞推算法往往使譜估值出現“譜線分裂“與“頻率偏移”等問題，因而,又有各種改進的算法。其中,較著名的有傅格算法和馬普爾算法，但是所需的計算量較大。另外，在有噪聲的情況下，如何選定階數仍有待進一步探討。
